Question

GOAL is a quadrilateral in which \[GO\parallel AL\]. If \[\angle G=\angle O={{40}^{\circ }}\] what are the measures of \[\angle A\] and \[\angle L\].

Answer 1

Hint: In this problem, we are given that GOAL is a quadrilateral in which \[GO\parallel AL\]. If \[\angle G=\angle O={{40}^{\circ }}\], we have to find the measures of \[\angle A\] and \[\angle L\]. Here we can first draw the diagram. Here we have to use the interior angle property, where the sum of the internal and external angle in the same vertex is \[{{180}^{\circ }}\]. By using this property we can find the required angles.

Complete step by step answer:
 Here, we are given that GOAL is a quadrilateral in which \[GO\parallel AL\]. If \[\angle G=\angle O={{40}^{\circ }}\], we have to find the measures of \[\angle A\] and \[\angle L\].
We can now draw the diagram.

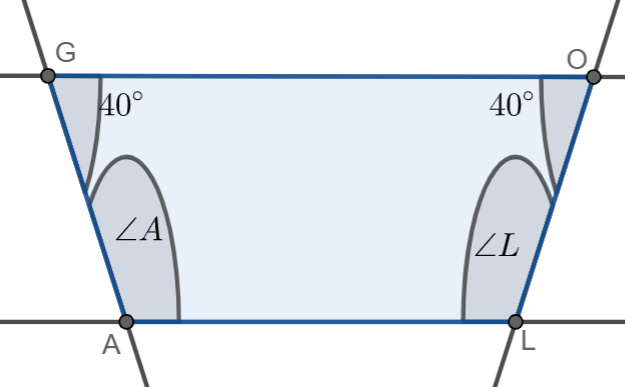
Here we can use the property of interior angle.
We know that the interior angle property is where the sum of the internal and external angle in the same vertex is \[{{180}^{\circ }}\].
We can now find the measure of \[\angle A\],
\[\Rightarrow \angle A+\angle O={{180}^{\circ }}\]
We can now substitute the given measure and simplify it, we get
\[\begin{align}
  & \Rightarrow \angle A+{{40}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle A={{180}^{\circ }}-{{40}^{\circ }}={{140}^{\circ }} \\
\end{align}\]
The measure of \[\angle A={{140}^{\circ }}\]
We can now find the measure of \[\angle L\],
\[\Rightarrow \angle G+\angle L={{180}^{\circ }}\]
We can now substitute the given measure and simplify it, we get
\[\begin{align}
  & \Rightarrow \angle L+{{40}^{\circ }}={{180}^{\circ }} \\
 & \Rightarrow \angle L={{180}^{\circ }}-{{40}^{\circ }}={{140}^{\circ }} \\
\end{align}\]
The measure of \[\angle L={{140}^{\circ }}\]
Therefore, the measure of\[\angle A=\angle L={{140}^{\circ }}\]

Note: We should always remember the interior angle property that the interior angle property is where the sum of internal and external angle in the same vertex is \[{{180}^{\circ }}\]. So if we have one of the ongles, then we can substitute in the sum to get the value of another angle.