Question

How do you graph \[\left( {{e^x}} \right).\sin \left( x \right)\]?

Answer 1

Hint: In order to solve this question first, we assume a function equal to the given function as a given relation. Then we find the zeros of the function and the period of the function with the extreme values of the function. We also check whether the function is passing through origin or not.

Complete step-by-step answer:
Let, the given function is:-
\[f\left( x \right) = \left( {{e^x}} \right).\sin \left( x \right)\]
To solve this question first we find all the zeros of the function.
The function is the multiplication of two functions that are an exponent function and a trigonometric function. Exponent functions are not zero and \[\sin \left( x \right)\] are the function which is 0 after a interval so the zeros of this function is same as the zeros of \[\sin \left( x \right)\] function.
The zeros of this function are \[x = \] an integral multiple of \[\pi \].
Sin function is a periodic function and it is also changing the sign of the function.
There are local extreme values in \[\left( {2n\pi ,\left( {2n + 2} \right)\pi } \right)\].
In this way we are able to plot the graph of any of the functions.
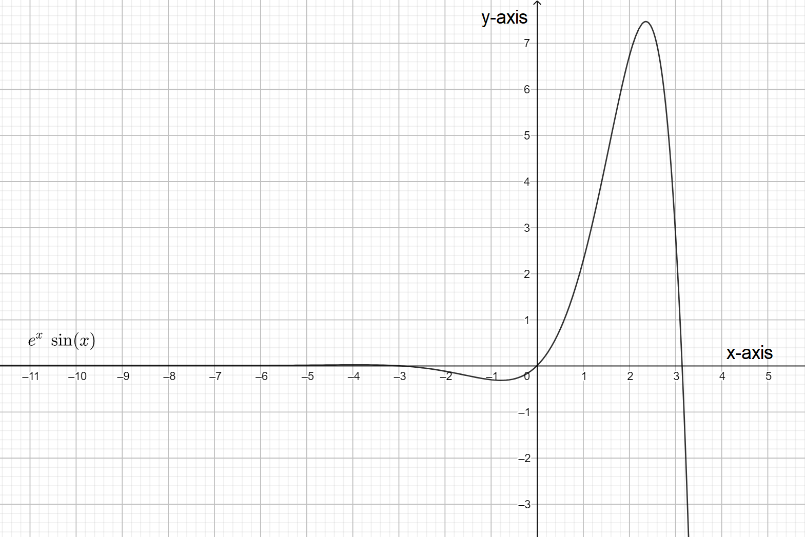
The graph of the given equation is.

Note:To solve these types of questions students must know few points to plot the graph. The points are-
Check whether the function is a periodic function or not if that is a periodic function then check the period of the function.
Check the zeros of the function. It means at which points the graph of the function cuts x-axis by putting y as 0.
Then check the extreme points of the curve and try to find that the curve is even or odd. And there are many points which I have to remember to solve this type of question.