Question

How do you graph the circle with center at $$\left(4,0\right)$$ and radius 3 and label the center and at least four points on the circle, then write the equation of the circle?

Answer 1

Hint: In this question we are asked to plot the circle with centre and radius given, We first Plot the center of the circle at $$\left(h,k\right)$$ and then count out from the center $$r$$ units in the four directions (up, down, left, and right). Then, connect those four points with a nice, round circle, and here $$h=4$$, $$k=0$$, and $$r=3$$ substitute the center and radius in the standard form of equation of circle which is given by $${\left(x-h\right)}^2+{\left(y-k\right)}^2=r^2$$.

Complete step by step solution:
A circle is the set of all points the same distance from a given point, the center of the circle. A radius, $$r$$, is the distance from that center point to the circle itself.
Now plotting the circle on the graph,
Given center $$\left(4,0\right)$$ and radius 3,
Place the center of the circle at $$\left(4,0\right)$$, which is shown in the figure below,

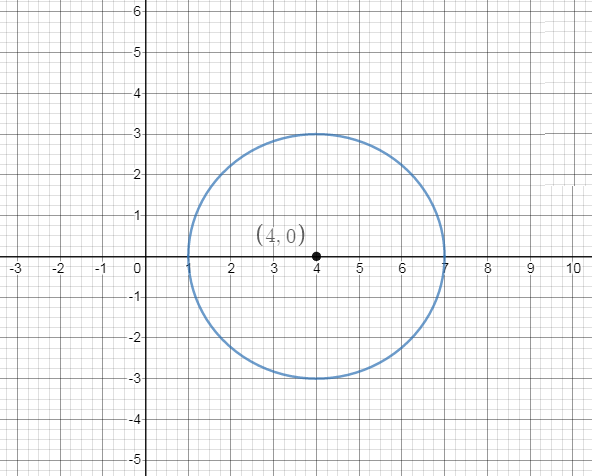
Plot the radius points on the coordinate plane, which is given as 3,

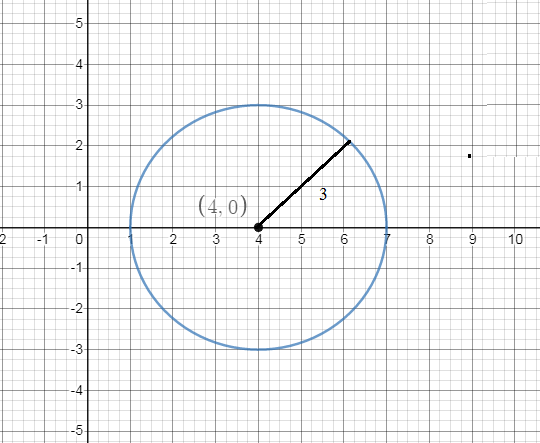
Now count 3 units up, down, left, and right from the center at $$\left(4,0\right)$$to plot the four points on the circle
Count 3 units right, i.e., add 3 units to the $$x$$-coordinate of the center we get,
$$\Rightarrow \left(4+3,0+0\right)=\left(7,0\right)$$,
Now count 3 units left i.e., subtract 3 units from the $$x$$-coordinate of the center we get,
$$\Rightarrow \left(4-3,0+0\right)=\left(1,0\right)$$,
Now count 3 units up, i.e., add 3 units to the $$y$$-coordinate of the center we get,
$$\Rightarrow \left(4+0,0+3\right)=\left(4,3\right)$$,
Now count 3 units down, subtract 3 units to the $$y$$-coordinate of the center we get,$$\Rightarrow \left(4+0,0-3\right)=\left(4,-3\right)$$,
 This means that we should have points at, $$\left(7,0\right)$$, $$\left(1,0\right)$$, $$\left(4,3\right)$$ and $$\left(4,-3\right)$$.
Connect the dots to the graph of the circle with a round, smooth curve.

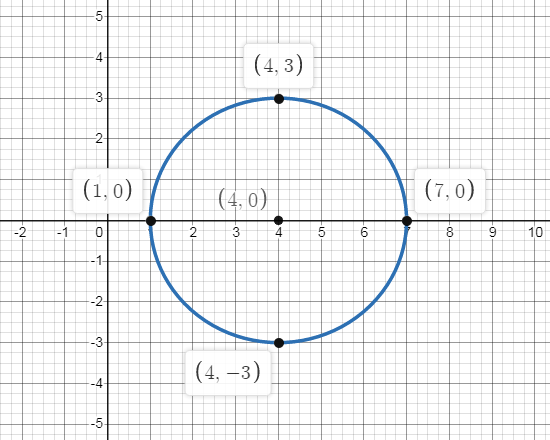
Now we know that the equation of circle with center $$\left(h,k\right)$$and radius $$r$$is given by $${\left(x-h\right)}^2+{\left(y-k\right)}^2=r^2$$, so here center $$\left(4,0\right)$$ and radius 3, substituting the values in the equation we get,
$$\Rightarrow {\left(x-4\right)}^2+{\left(y-0\right)}^2=3^2$$,
Now simplifying we get,
$$\Rightarrow {\left(x-4\right)}^2+y^2=9$$.
So, the equation of the circle is $${\left(x-4\right)}^2+y^2=9$$.

$$\therefore$$ The required graph for the circle with center $$\left(4,0\right)$$and radius 3 will be shown as,

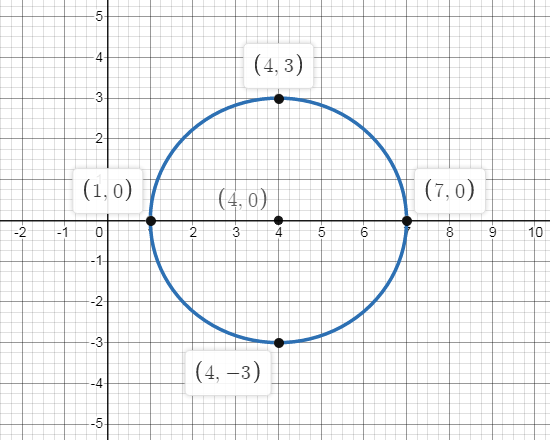
and the equation of circle with center $$\left(4,0\right)$$and radius 3 will be equal to$${\left(x-4\right)}^2+y^2=9$$.

Note:
Graphing circles requires two things: the coordinates of the center point, and the radius of a circle. While plotting the circle on the graph we have to remember to switch the sign of the $$h$$ and $$k$$from inside the parentheses in the equation. This is necessary because the $$h$$ and $$k$$ are inside the grouping symbols, which means that the shift happens opposite from what we would think.