
How do you graph the equation \[y = - 4\] by making a table and what is its domain and range?
Answer
448.8k+ views
Hint: Here, the value of \[y\] is constant, so we will select some arbitrary values of \[x\] to find the different coordinate points. To do this, we will make a table consisting of values of \[x\] and corresponding values of \[y\]. Then, we will draw the graph of the equation using the points and then find the domain and range.
Complete step by step solution:
The equation given to us is \[y = - 4\]. We have to graph this equation and find its domain and range. Let us assume \[f(x) = y = - 4\].
Let us take \[x = 0\]. We get \[y = - 4\].
If we take \[x = - 4\], we get \[y = - 4\] again. So, no matter what value of \[x\] we take, we will always get the value of \[y\] as \[y = - 4\]. Let us form a table and graph the equation \[y = - 4\] using the table.
So, we get the points as \[A( - 4, - 4)\], \[B(0, - 4)\] and \[C(3, - 4)\]. Now we will draw the graph by plotting these points
We get the graph as follows:
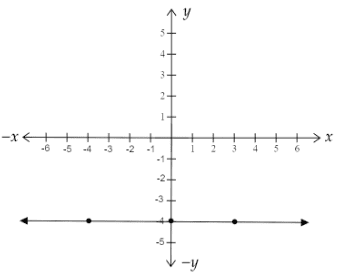
We can see from the above graph that the graph of \[f(x)\] is a horizontal line passing through the point \[y = - 4\]. This is because the function \[f\] is a constant function.
Now, let us find the domain and range of the function \[f\].
The domain of a function \[f\] is the set of all inputs of the function. In the given function, we consider all real numbers as inputs. So, the domain is the entire real line \[\mathbb{R} = ( - \infty ,\infty )\]
The range of a function \[f\] is the set of all outputs of the function. In the given function, we have only one output which is \[ - 4\]. So, the range is \[\{ - 4\} \].
Note:
A constant function is defined a function \[f:\mathbb{R} \to \mathbb{R}\], where \[f(x) = c\], for all \[x \in \mathbb{R}\] and \[c\] is a constant. The graph of a constant function will be a line parallel to the \[x - \]axis. It lies above the \[x - \] axis if \[c\] is positive, below the \[x - \] axis if \[c\] is negative and coincident with the \[x - \] axis if \[c\] is zero. In the given problem, \[c = - 4\] which is negative and so, we get a line below the \[x - \] axis.
Complete step by step solution:
The equation given to us is \[y = - 4\]. We have to graph this equation and find its domain and range. Let us assume \[f(x) = y = - 4\].
Let us take \[x = 0\]. We get \[y = - 4\].
If we take \[x = - 4\], we get \[y = - 4\] again. So, no matter what value of \[x\] we take, we will always get the value of \[y\] as \[y = - 4\]. Let us form a table and graph the equation \[y = - 4\] using the table.
| \[x\] | \[f(x) = y\] |
| \[-4\] | \[ - 4\] |
| 0 | \[ - 4\] |
| 3 | \[ - 4\] |
So, we get the points as \[A( - 4, - 4)\], \[B(0, - 4)\] and \[C(3, - 4)\]. Now we will draw the graph by plotting these points
We get the graph as follows:

We can see from the above graph that the graph of \[f(x)\] is a horizontal line passing through the point \[y = - 4\]. This is because the function \[f\] is a constant function.
Now, let us find the domain and range of the function \[f\].
The domain of a function \[f\] is the set of all inputs of the function. In the given function, we consider all real numbers as inputs. So, the domain is the entire real line \[\mathbb{R} = ( - \infty ,\infty )\]
The range of a function \[f\] is the set of all outputs of the function. In the given function, we have only one output which is \[ - 4\]. So, the range is \[\{ - 4\} \].
Note:
A constant function is defined a function \[f:\mathbb{R} \to \mathbb{R}\], where \[f(x) = c\], for all \[x \in \mathbb{R}\] and \[c\] is a constant. The graph of a constant function will be a line parallel to the \[x - \]axis. It lies above the \[x - \] axis if \[c\] is positive, below the \[x - \] axis if \[c\] is negative and coincident with the \[x - \] axis if \[c\] is zero. In the given problem, \[c = - 4\] which is negative and so, we get a line below the \[x - \] axis.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

State and prove Bernoullis theorem class 11 physics CBSE

What organs are located on the left side of your body class 11 biology CBSE

Write down 5 differences between Ntype and Ptype s class 11 physics CBSE




