
How do you graph the equation \[y - 8 = - x\] by making a table and what is its domain and range?
Answer
432.3k+ views
Hint: Here firstly we need to arrange the equation in \[y\] terms for finding the value of \[x\] and \[y\] considering them as different values and drawing table by giving random values for \[x\] and finding value of \[y\] . Later on we will plot the graph \[x\] versus \[y\] with the help of values from the table. The graph can also be drawn using the intercept method and lastly we will find the domain and the range.
Formula: By using the table of function we will take the random value of \[x\] and substitute in the equation for finding the value of \[y\] . Later on after finding the sufficient points we will sketch the graph
Complete step-by-step answer:
We are given the equation \[y - 8 = - x\] . So firstly we need to solve for \[y\]
After adding \[8\] to both the sides of the equation we will get
\[y - 8 + 8 = - x + 8\]
After further simplification we get
\[y = - x + 8\]
Now we will draw a table by taking random values of x and putting in the equation to get value of y
Thus after getting various coordinates we will sketch a graph for these coordinates
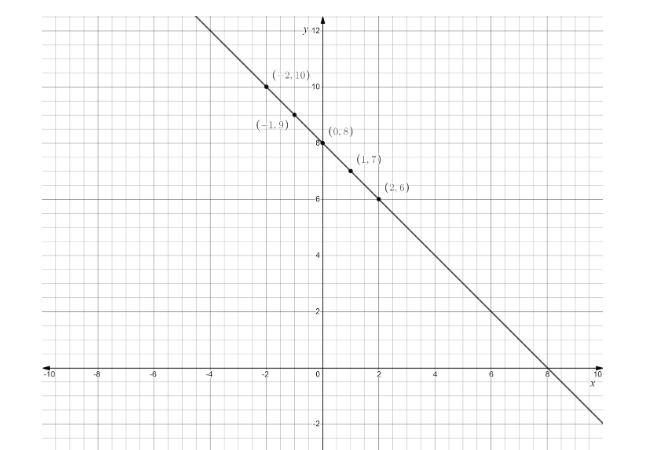
We will expand the line by matching the points one line and we will notice \[y\] is having all the real numbers.
Now we will find the domain and range and as we know that function domain and range are all the real numbers as there is nothing we can put for \[x\] and y that won’t work. That is the reason why the graph extends forever in the \[x\] directions and also extends forever in the \[y\] direction. Hence domain and range is all the real numbers.
Hence domain is \[( - \infty , + \infty )\] and range is \[( - \infty , + \infty )\]
Note: Here in this question we are given a linear equation with two variables \[x\] and y where \[x\] is measures along \[x\] axis and \[y\] is measured along \[y\] axis while tracing the given equation. Remember we need to arrange the equation in \[y\] terms so that different \[y\] values can be calculated by taking random values of \[x\] .Mark the points carefully for getting the correct graph for the given equation.
Formula: By using the table of function we will take the random value of \[x\] and substitute in the equation for finding the value of \[y\] . Later on after finding the sufficient points we will sketch the graph
Complete step-by-step answer:
We are given the equation \[y - 8 = - x\] . So firstly we need to solve for \[y\]
After adding \[8\] to both the sides of the equation we will get
\[y - 8 + 8 = - x + 8\]
After further simplification we get
\[y = - x + 8\]
Now we will draw a table by taking random values of x and putting in the equation to get value of y
| \[x\] | \[ - 2\] | \[ - 1\] | \[0\] | \[1\] | \[2\] |
| y | \[10\] | \[9\] | \[8\] | \[7\] | \[6\] |
Thus after getting various coordinates we will sketch a graph for these coordinates

We will expand the line by matching the points one line and we will notice \[y\] is having all the real numbers.
Now we will find the domain and range and as we know that function domain and range are all the real numbers as there is nothing we can put for \[x\] and y that won’t work. That is the reason why the graph extends forever in the \[x\] directions and also extends forever in the \[y\] direction. Hence domain and range is all the real numbers.
Hence domain is \[( - \infty , + \infty )\] and range is \[( - \infty , + \infty )\]
Note: Here in this question we are given a linear equation with two variables \[x\] and y where \[x\] is measures along \[x\] axis and \[y\] is measured along \[y\] axis while tracing the given equation. Remember we need to arrange the equation in \[y\] terms so that different \[y\] values can be calculated by taking random values of \[x\] .Mark the points carefully for getting the correct graph for the given equation.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
When people say No pun intended what does that mea class 8 english CBSE

How many ounces are in 500 mL class 8 maths CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

Which king started the organization of the Kumbh fair class 8 social science CBSE

What is BLO What is the full form of BLO class 8 social science CBSE

Advantages and disadvantages of science




