
How do you graph using the intercepts for 5x – 5y = 10?
Answer
546.3k+ views
Hint: Here in this question, we will use the general form of the equation of slope and intercept to solve this problem. The general form of this equation is y = mx + c where m is the slope and c is the constant here that tells you to shift up or down the graph by b units. This is basically slope-intercept form which we will be using in this question.
Complete step by step answer:
Now let’s solve the question.
As we know about the slope-intercept form that it is a general form of a straight line and is expressed as y = mx + c where ‘m’ is a slope and c is a constant and intercepts are m and c.
For plotting the straight line, first, we need to convert the given equation in a slope-intercept form. Let’s see how!
Write the equation from the question.
$ \Rightarrow $ 5x - 5y = 10
Take 5 common from the left-hand side:
$ \Rightarrow $ 5(x - y) = 10
Now take 5 to the other side:
$ \Rightarrow $ x – y = $ \dfrac{10}{5} $
$ \Rightarrow $ x – y = 5
Take 5 to the left side and –y to the right side of the equation. We get:
$ \Rightarrow y=x-5.....(i) $
Therefore, we have got our equation in the slope-intercept form i.e. y = mx + c.
Here, m = 1 and c = -5 .
Now, we have to find the intercepts for x and y.
Let’s find y-intercept first. Substitute x = 0 in equation(i) we get:
$ \Rightarrow $ y = (0) - 5
Now we get the value of ‘y’ as:
$ \Rightarrow $ y = -5
$ \therefore $ y-intercept form is: $ \left( 0,-5 \right) $
Similarly, find x-intercept. Put y = 0 in equation(i) we get:
$ \Rightarrow $ (0) = x – 5
Now the value of x will be:
$ \Rightarrow $ x = 5
$ \therefore $ x-intercept will be: (5,0)
Now, let’s plot the graph of the equation given in the question with the help of the intercepts.
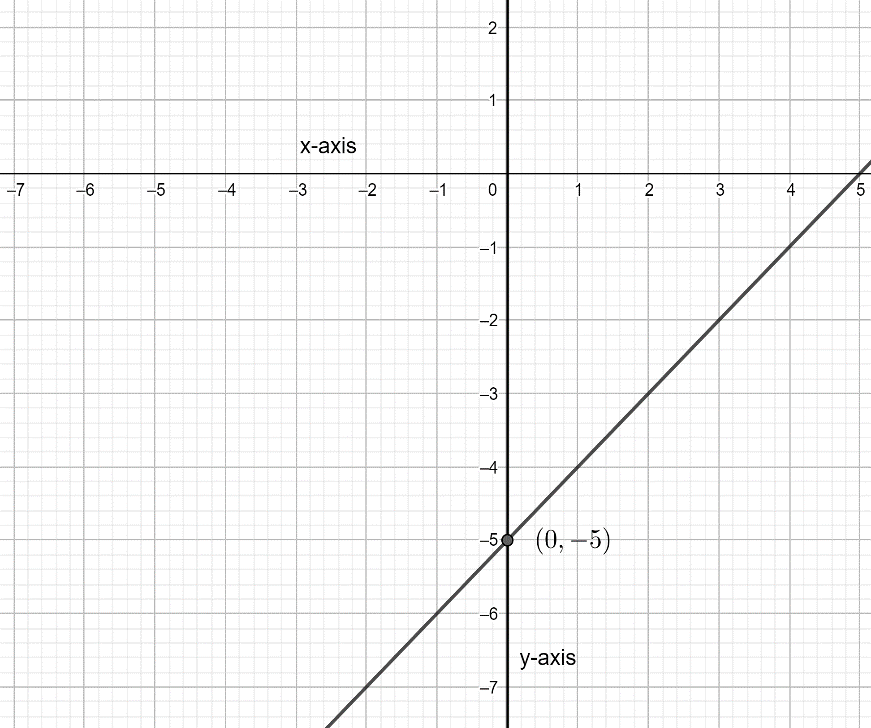
The graph above is of y-intercept: (0,-5)
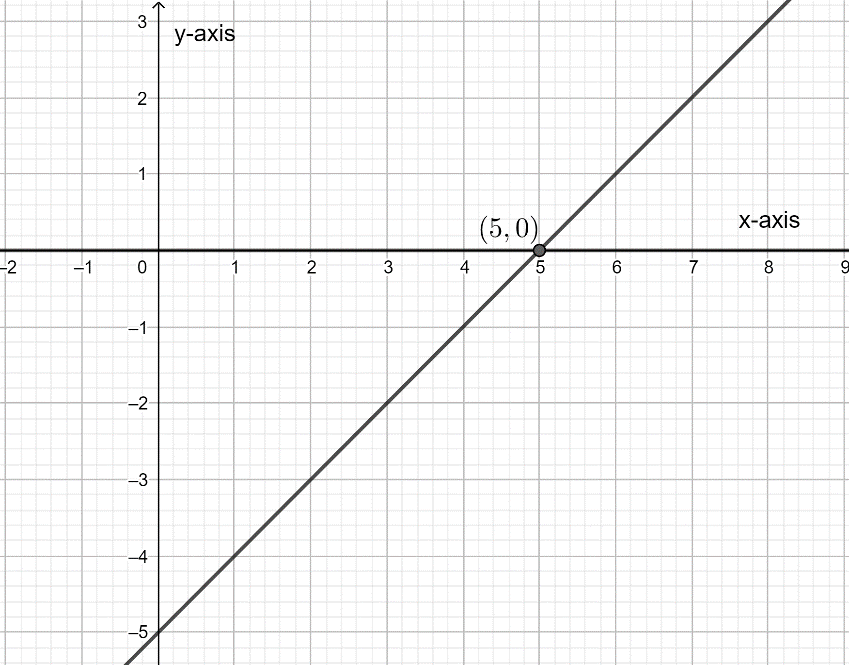
The graph above is of x-intercept: (5,0)
Note:
In this question particularly, we have to use the slope-intercept form as it is asked to graph the equation by using intercepts. Else the question can be solved by substitution also. Plot the graph neatly.
Complete step by step answer:
Now let’s solve the question.
As we know about the slope-intercept form that it is a general form of a straight line and is expressed as y = mx + c where ‘m’ is a slope and c is a constant and intercepts are m and c.
For plotting the straight line, first, we need to convert the given equation in a slope-intercept form. Let’s see how!
Write the equation from the question.
$ \Rightarrow $ 5x - 5y = 10
Take 5 common from the left-hand side:
$ \Rightarrow $ 5(x - y) = 10
Now take 5 to the other side:
$ \Rightarrow $ x – y = $ \dfrac{10}{5} $
$ \Rightarrow $ x – y = 5
Take 5 to the left side and –y to the right side of the equation. We get:
$ \Rightarrow y=x-5.....(i) $
Therefore, we have got our equation in the slope-intercept form i.e. y = mx + c.
Here, m = 1 and c = -5 .
Now, we have to find the intercepts for x and y.
Let’s find y-intercept first. Substitute x = 0 in equation(i) we get:
$ \Rightarrow $ y = (0) - 5
Now we get the value of ‘y’ as:
$ \Rightarrow $ y = -5
$ \therefore $ y-intercept form is: $ \left( 0,-5 \right) $
Similarly, find x-intercept. Put y = 0 in equation(i) we get:
$ \Rightarrow $ (0) = x – 5
Now the value of x will be:
$ \Rightarrow $ x = 5
$ \therefore $ x-intercept will be: (5,0)
Now, let’s plot the graph of the equation given in the question with the help of the intercepts.
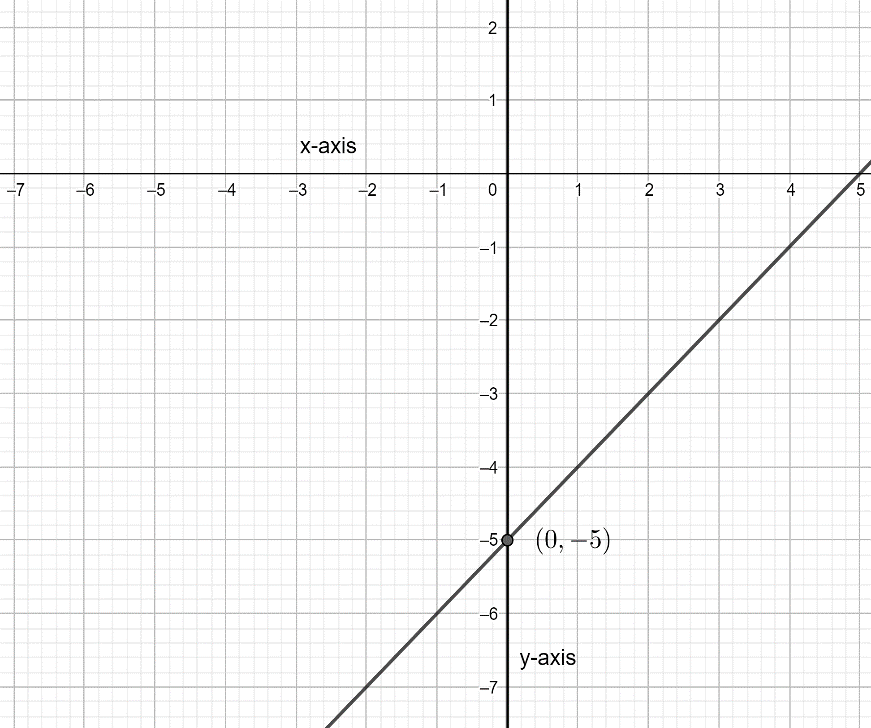
The graph above is of y-intercept: (0,-5)
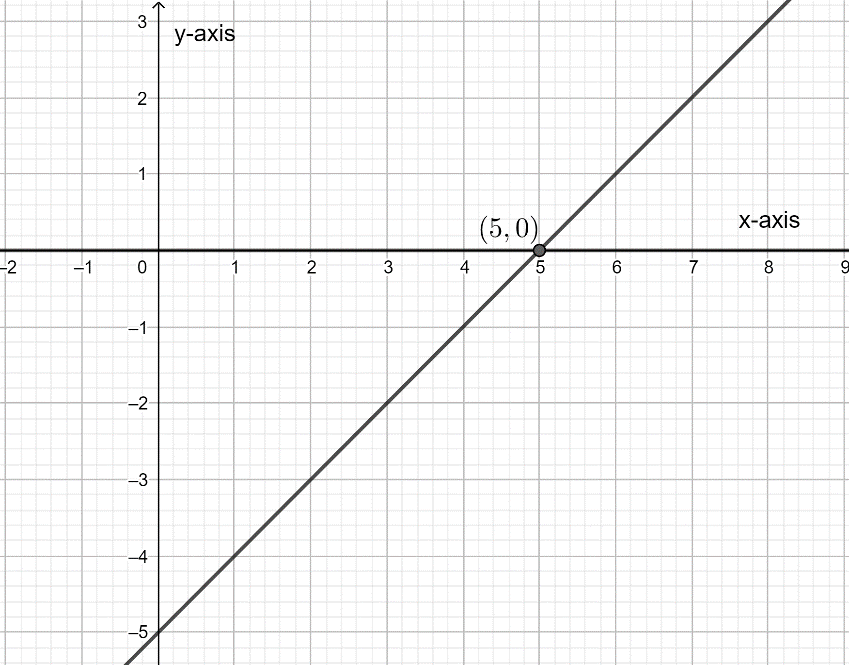
The graph above is of x-intercept: (5,0)
Note:
In this question particularly, we have to use the slope-intercept form as it is asked to graph the equation by using intercepts. Else the question can be solved by substitution also. Plot the graph neatly.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




