
How do you graph
Answer
462k+ views
Hint: Here, we need to graph the given line. We will take the abscissa and ordinate 0 to find the intercepts, and use them to draw the graph of the given equation. The abscissa of a point
Complete step-by-step solution:
First, we will find the intercepts of the given line.
Rewriting the equation, we get
Substituting 0 for
Therefore, we get
The
This means that the line touches the
Substituting 0 for
Therefore, we get
This is incorrect.
The given line has no
Therefore, there is no point on the given line that has the abscissa 0.
This means that the line does not touch the
When two straight lines do not touch each other at any point, they are called parallel lines.
This means that the graph of the line
Now, we will draw the graph of the given line.
The graph of the line
The value of
Drawing the graph of the line
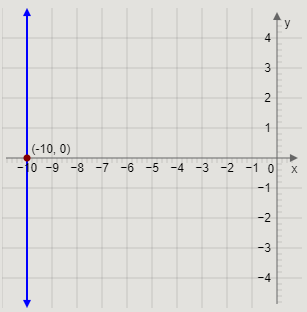
This is the required graph of the line
Note:
We can also rewrite the equation using the intercept form of a line.
The intercept form of a line is given by
Dividing both sides of the given equation by
Here,
Complete step-by-step solution:
First, we will find the intercepts of the given line.
Rewriting the equation, we get
Substituting 0 for
Therefore, we get
The
This means that the line touches the
Substituting 0 for
Therefore, we get
This is incorrect.
The given line has no
Therefore, there is no point on the given line that has the abscissa 0.
This means that the line does not touch the
When two straight lines do not touch each other at any point, they are called parallel lines.
This means that the graph of the line
Now, we will draw the graph of the given line.
The graph of the line
The value of
Drawing the graph of the line

This is the required graph of the line
Note:
We can also rewrite the equation using the intercept form of a line.
The intercept form of a line is given by
Dividing both sides of the given equation by
Here,
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

In northern hemisphere 21st March is called as A Vernal class 11 social science CBSE




