
How do you graph
Answer
450.9k+ views
Hint: To solve this we need to give the values of ‘x’ and we can find the values of ‘y’. Otherwise we can find the coordinate of the given equation lying on the line of x- axis, we can find this by substituting the value of ‘y’ is equal to zero (x-intercept). Similarly we can find the coordinate of the equation lying on the line of y- axis, we can find this by substituting the value of ‘x’ equal to zero (y-intercept).
Complete step-by-step answer:
Given,
To find the x-intercept. That is the value of ‘x’ at
Thus we have a coordinate of the equation which lies on the line of x-axis. The coordinate is
To find the y-intercept. That is the value of ‘y’ at
Divide by ‘-4’ on both sides of the equation,
Thus we have a coordinate of the equation which lies on the line of y-axis. The coordinate is
Thus we have the coordinates
Let’s plot a graph for this coordinates,
We take scale
x-axis= 1 unit = 2 units
y-axis= 1 unit = 1 units
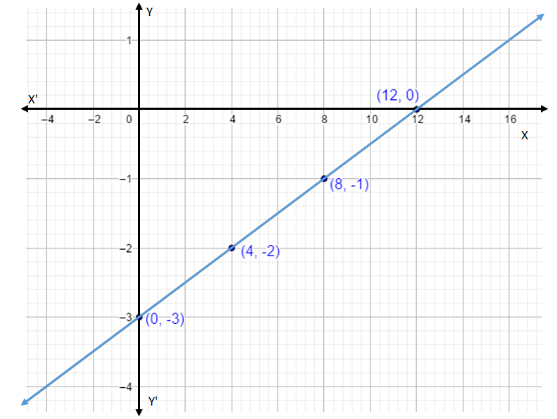
All we did was expand the line touching the coordinates
Without calculation we have found out few more coordinates are
Note: Intercept method is an easy method for drawing graphs. A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.
Complete step-by-step answer:
Given,
To find the x-intercept. That is the value of ‘x’ at
Thus we have a coordinate of the equation which lies on the line of x-axis. The coordinate is
To find the y-intercept. That is the value of ‘y’ at
Divide by ‘-4’ on both sides of the equation,
Thus we have a coordinate of the equation which lies on the line of y-axis. The coordinate is
Thus we have the coordinates
Let’s plot a graph for this coordinates,
We take scale
x-axis= 1 unit = 2 units
y-axis= 1 unit = 1 units

All we did was expand the line touching the coordinates
Without calculation we have found out few more coordinates are
Note: Intercept method is an easy method for drawing graphs. A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

Advantages and disadvantages of science

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

How many ten lakhs are in one crore-class-8-maths-CBSE

What led to the incident of Bloody Sunday in Russia class 8 social science CBSE





