
How do you graph \[x = {y^2} - 2y\] using a table of values?
Answer
437.4k+ views
Hint: We need to draw the graph ‘x’ versus ‘y’. We give the random values for ‘x’ and we find the value of ‘y’. We can give all real numbers for the value of ‘x’. Thus we will have coordinate points (x, y). Hence, we can plot the graph by using the values. We can also draw the graph using the intercept method. But here we have a function which is passing through origin. So we use tables to draw the graph.
Complete step-by-step answer:
Given \[x = {y^2} - 2y\] .
Rearranging the equation we have
\[y = 1 - x\]
Let's give the values for ‘x’ and we find the value of ‘y’.
Put \[x = 1\] in \[x = {y^2} - 2y\] we have,
\[1 = {y^2} - 2y\]
\[{y^2} - 2y - 1 = 0\]
We use quadratic formula \[y = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\] , where \[a = 1\] , \[b = - 2\] and \[c = - 1\] .
\[y = \dfrac{{ - ( - 2) \pm \sqrt {{{( - 2)}^2} - 4(1)( - 1)} }}{{2(1)}}\]
\[y = \dfrac{{2 \pm \sqrt {4 + 4} }}{2}\]
\[y = \dfrac{{2 \pm \sqrt 8 }}{2}\]
\[y = \dfrac{{2 \pm \sqrt {4 \times 2} }}{2}\]
\[y = \dfrac{{2 \pm 2\sqrt 2 }}{2}\]
\[y = \dfrac{{2\left( {1 \pm \sqrt 2 } \right)}}{2}\]
\[y = 1 \pm \sqrt 2 \]
That is
\[ \Rightarrow y = 1 + \sqrt 2 \] and \[y = 1 - \sqrt 2 \]
\[ \Rightarrow y = 1 + 1.414\] and \[y = 1 - 1.414\]
\[ \Rightarrow y = 2.414\] and \[y = - 0.414\]
Rounding off the decimal points we have
\[ \Rightarrow y = 2.41\] and \[y = - 0.41\]
Thus we have coordinate point \[(1,2.41)\] and \[(1, - 0.41)\] .
Put \[x = - 1\] in \[x = {y^2} - 2y\] we have,
\[ - 1 = {y^2} - 2y\]
\[{y^2} - 2y + 1 = 0\]
This is of the form \[{a^2} - 2ab + {b^2} = {(a - b)^2}\] , where \[a = y\] and \[b = 1\] .
\[{(y - 1)^2} = 0\]
Thus we have
\[ \Rightarrow y = 1,1\]
Thus we have coordinate point \[( - 1,1)\] .
Put \[x = 2\] in \[x = {y^2} - 2y\] we have,
\[2 = {y^2} - 2y\]
\[{y^2} - 2y - 2 = 0\]
We use quadratic formula \[y = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\] , where \[a = 1\] , \[b = - 2\] and \[c = - 2\] .
\[y = \dfrac{{ - ( - 2) \pm \sqrt {{{( - 2)}^2} - 4(1)( - 2)} }}{{2(1)}}\]
\[y = \dfrac{{2 \pm \sqrt {4 + 8} }}{2}\]
\[y = \dfrac{{2 \pm \sqrt {12} }}{2}\]
\[y = \dfrac{{2 \pm \sqrt {4 \times 3} }}{2}\]
\[y = \dfrac{{2 \pm 2\sqrt 3 }}{2}\]
\[y = \dfrac{{2\left( {1 \pm \sqrt 3 } \right)}}{2}\]
\[y = 1 \pm \sqrt 3 \]
That is
\[ \Rightarrow y = 1 + \sqrt 3 \] and \[y = 1 - \sqrt 3 \]
\[ \Rightarrow y = 1 + 1.732\] and \[y = 1 - 1.732\]
\[ \Rightarrow y = 2.732\] and \[y = - 0.732\]
Round off the decimal point we have,
\[ \Rightarrow y = 2.73\] and \[y = - 0.73\]
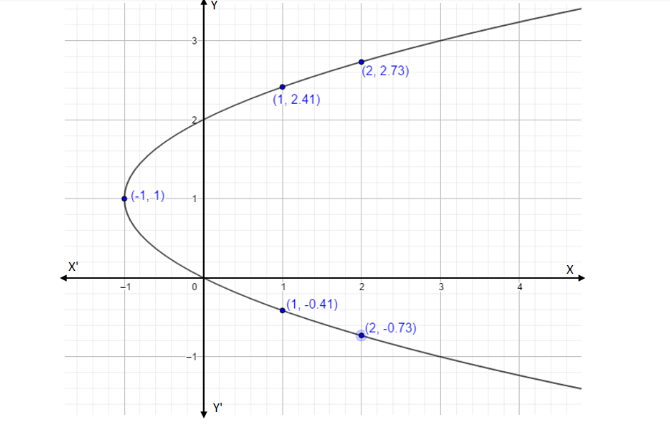
Thus we have coordinate points \[(2,2.73)\] and \[(2, - 0.73)\] .
Thus we have,
Let’s draw the graph for these coordinates,
Note: A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.
Complete step-by-step answer:
Given \[x = {y^2} - 2y\] .
Rearranging the equation we have
\[y = 1 - x\]
Let's give the values for ‘x’ and we find the value of ‘y’.
Put \[x = 1\] in \[x = {y^2} - 2y\] we have,
\[1 = {y^2} - 2y\]
\[{y^2} - 2y - 1 = 0\]
We use quadratic formula \[y = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\] , where \[a = 1\] , \[b = - 2\] and \[c = - 1\] .
\[y = \dfrac{{ - ( - 2) \pm \sqrt {{{( - 2)}^2} - 4(1)( - 1)} }}{{2(1)}}\]
\[y = \dfrac{{2 \pm \sqrt {4 + 4} }}{2}\]
\[y = \dfrac{{2 \pm \sqrt 8 }}{2}\]
\[y = \dfrac{{2 \pm \sqrt {4 \times 2} }}{2}\]
\[y = \dfrac{{2 \pm 2\sqrt 2 }}{2}\]
\[y = \dfrac{{2\left( {1 \pm \sqrt 2 } \right)}}{2}\]
\[y = 1 \pm \sqrt 2 \]
That is
\[ \Rightarrow y = 1 + \sqrt 2 \] and \[y = 1 - \sqrt 2 \]
\[ \Rightarrow y = 1 + 1.414\] and \[y = 1 - 1.414\]
\[ \Rightarrow y = 2.414\] and \[y = - 0.414\]
Rounding off the decimal points we have
\[ \Rightarrow y = 2.41\] and \[y = - 0.41\]
Thus we have coordinate point \[(1,2.41)\] and \[(1, - 0.41)\] .
Put \[x = - 1\] in \[x = {y^2} - 2y\] we have,
\[ - 1 = {y^2} - 2y\]
\[{y^2} - 2y + 1 = 0\]
This is of the form \[{a^2} - 2ab + {b^2} = {(a - b)^2}\] , where \[a = y\] and \[b = 1\] .
\[{(y - 1)^2} = 0\]
Thus we have
\[ \Rightarrow y = 1,1\]
Thus we have coordinate point \[( - 1,1)\] .
Put \[x = 2\] in \[x = {y^2} - 2y\] we have,
\[2 = {y^2} - 2y\]
\[{y^2} - 2y - 2 = 0\]
We use quadratic formula \[y = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\] , where \[a = 1\] , \[b = - 2\] and \[c = - 2\] .
\[y = \dfrac{{ - ( - 2) \pm \sqrt {{{( - 2)}^2} - 4(1)( - 2)} }}{{2(1)}}\]
\[y = \dfrac{{2 \pm \sqrt {4 + 8} }}{2}\]
\[y = \dfrac{{2 \pm \sqrt {12} }}{2}\]
\[y = \dfrac{{2 \pm \sqrt {4 \times 3} }}{2}\]
\[y = \dfrac{{2 \pm 2\sqrt 3 }}{2}\]
\[y = \dfrac{{2\left( {1 \pm \sqrt 3 } \right)}}{2}\]
\[y = 1 \pm \sqrt 3 \]
That is
\[ \Rightarrow y = 1 + \sqrt 3 \] and \[y = 1 - \sqrt 3 \]
\[ \Rightarrow y = 1 + 1.732\] and \[y = 1 - 1.732\]
\[ \Rightarrow y = 2.732\] and \[y = - 0.732\]
Round off the decimal point we have,
\[ \Rightarrow y = 2.73\] and \[y = - 0.73\]
Thus we have coordinate points \[(2,2.73)\] and \[(2, - 0.73)\] .
Thus we have,
| \[x\] | \[1\] | \[1\] | \[ - 1\] | \[2\] | \[2\] |
| \[y\] | \[2.41\] | \[ - 0.41\] | \[1\] | \[2.73\] | \[ - 0.73\] |
Let’s draw the graph for these coordinates,

Note: A graph shows the relation between two variable quantities, it contains two axes perpendicular to each other namely the x-axis and the y-axis. Each variable is measured along one of the axes. In the question, we are given one linear equation containing two variables namely x and y, x is measured along the x-axis and y is measured along the y-axis while tracing the given equations.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
List some examples of Rabi and Kharif crops class 8 biology CBSE

State the differences between manure and fertilize class 8 biology CBSE

Public administration is concerned with the administration class 8 social science CBSE

What led to the incident of Bloody Sunday in Russia class 8 social science CBSE

What is the tagline of Swachh Bharat Abhiyaan A Sabka class 8 social studies CBSE

State whether true or false Every rhombus is a square class 8 maths CBSE




