Question

How do you graph $y = \cot \left( {x - \dfrac{\pi }{5}} \right)$?

Answer 1

Hint: Here, we are given the cotangent function. We know that cotangent is the periodic function. We will first use the general form equation of the cotangent function to find certain values such as the period, phase shift and vertical shift of the function.

Formula used:
$y = A\cot \left( {Bx - C} \right) + D$,where, $A$ is the vertical stretch factor, $B$ is used to find the period $P = \dfrac{\pi }{{\left| B \right|}}$, $ - \dfrac{C}{B}$ is the phase shift and $D$ is the vertical shift.

Complete step by step solution:
We will first use the general equation of the cotangent function and compare it with the given one to find the period, phase shift and vertical shift of the function.
The general form of cotangent equation is: $y = A\cot \left( {Bx - C} \right) + D$.
If we compare it with the given function $y = \cot \left( {x - \dfrac{\pi }{5}} \right)$ , we get $A = 1$ and $B = 1$, $C = - \dfrac{\pi }{5}$ and $D = 0$.
We know that cotangent function has no amplitude.
Thus, we can say that
The period of the function $y = \cot \left( {x - \dfrac{\pi }{5}} \right)$ is $P = \dfrac{\pi }{{\left| B \right|}} = \dfrac{\pi }{1} = \pi $ .
Phase shift of the function $y = \cot \left( {x - \dfrac{\pi }{5}} \right)$ is $ - \dfrac{C}{B} = - \dfrac{{\left( { - \dfrac{\pi }{5}} \right)}}{1} = \dfrac{\pi }{5}$. This value is positive and thus the shift is to the right side.
Vertical shift of the function $y = \cot \left( {x - \dfrac{\pi }{5}} \right)$ is $D = 0$.
By using this information, the graph of the given function $y = \cot \left( {x - \dfrac{\pi }{5}} \right)$ can be obtained as:

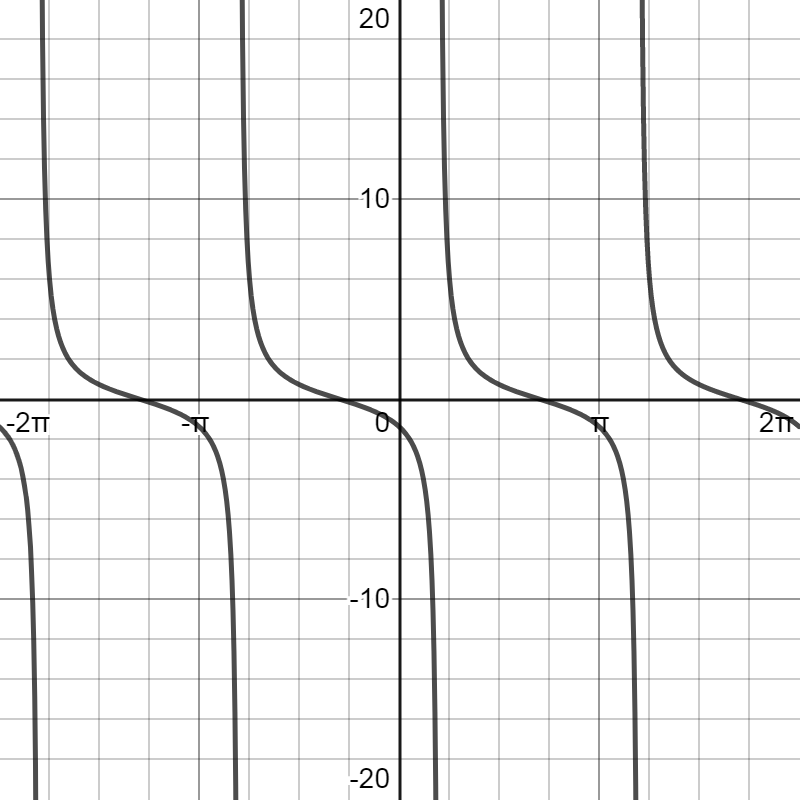
Note: The important thing to note here is that the shape of the given function $y = \cot \left( {x - \dfrac{\pi }{5}} \right)$ is same as that of the simple cotangent function $y = \cot x$. However, here $\dfrac{\pi }{5}$ is added to the angle $x$. This will result in the phase shift of the graph to $\dfrac{\pi }{5}$ units to the right. We have also seen here that the given cotangent function is a periodic function that repeats its values in regular intervals or periods.