Question

How do you find the slope for $5x-4y=20$?

Answer 1

Hint: Change of form of the given equation will give the slope of the line $5x-4y=20$. We change it to the form of $y=mx+k$ to find the slope m. At the end we get into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$ to find the x intercept, and y intercept of the line as p and q respectively. Then we place the line on the graph based on that.

Complete step by step answer:
We are taking the general equation to understand the slope form of the line $5x-4y=20$.
The given equation $5x-4y=20$ is of the form $ax+by=c$. Here a, b, c are the constants.
We convert the form to $y=mx+k$. m is the slope of the line.
So, converting the equation we get
$\begin{align}
  & 5x-4y=20 \\
 & \Rightarrow y=\dfrac{5x-20}{4}=\dfrac{5}{4}x-5 \\
\end{align}$
This gives the slope of the line $5x-4y=20$ as $\dfrac{5}{4}$.
We convert the given equation into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$. From the form we get that the x intercept, and y intercept of the line will be p and q respectively.
The given equation is $5x-4y=20$. Converting into the form of $\dfrac{x}{p}+\dfrac{y}{q}=1$, we get
$\begin{align}
  & 5x-4y=20 \\
 & \Rightarrow \dfrac{5x}{20}+\dfrac{-4y}{20}=1 \\
 & \Rightarrow \dfrac{x}{4}+\dfrac{y}{-5}=1 \\
\end{align}$
Therefore, the x intercept, and y intercept of the line $5x-4y=20$ is 4 and $-5$ respectively.
The intersecting points for the line $5x-4y=20$ with the axes will be $\left( 4,0 \right)$ and $\left( 0,-5 \right)$.

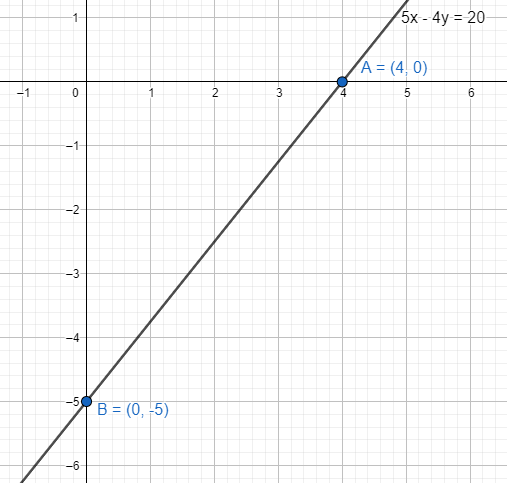
Note: A line parallel to the X-axis does not intersect the X-axis at any finite distance and hence we cannot get any finite x-intercept of such a line. Same goes for lines parallel to the Y-axis. In case of slope of a line the range of the slope is 0 to $\infty $.