Question

How do you graph $r=-2\sin \theta $?

Answer 1

Hint: We explain the number of ways the position of a point or equation can be expressed in different forms. To form the graph of $r=-2\sin \theta $, we need to find its rectangular form. We also explain the ways the representation works for polar and cartesian form. Then we convert the given equation into rectangular form using the relations $x=r\cos \theta ;y=r\sin \theta $.

Complete step by step answer:
There are always two ways to represent any point equation in our general 2-D and 3-D surfaces. One being polar form and the other one being the cartesian form. The other name of the cartesian form is rectangular form.
In case of polar form, we use the distance and the angle from the origin to get the position of the point or curve.
The given equation $r=-2\sin \theta $ is a representation of the polar form. r represents the distance and $\theta $ represents the angle.
In case of rectangular form, we use the coordinates from the origin to get the position of the point or curve. For two dimensional things we have X-Y and for three dimensional things we have X-Y-Z. We take the perpendicular distances from the axes.
We need to convert the given equation $r=-2\sin \theta $ into the rectangular form.
The relation between these two forms in two-dimensional is
$x=r\cos \theta ;y=r\sin \theta ;{{x}^{2}}+{{y}^{2}}={{r}^{2}}$.
From the relations we get $\sin \theta =\dfrac{y}{r}$.
We now replace the value of $\sin \theta =\dfrac{y}{r}$ in the equation $r=-2\sin \theta $ to get
\[\begin{align}
  & r=-2\sin \theta \\
 & \Rightarrow r=-2\left( \dfrac{y}{r} \right) \\
 & \Rightarrow r=\dfrac{-2y}{r} \\
 & \Rightarrow -2y={{r}^{2}} \\
\end{align}\]
We now replace the value of ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$ for the equation \[-2y={{r}^{2}}\]. The revised equation becomes \[-2y={{r}^{2}}={{x}^{2}}+{{y}^{2}}\].
The equation is an equation of circle \[{{x}^{2}}+{{y}^{2}}=-2y\].
Reforming the equation, we get \[{{x}^{2}}+{{\left( y+1 \right)}^{2}}=1\]. The centre is $\left( 0,-1 \right)$.

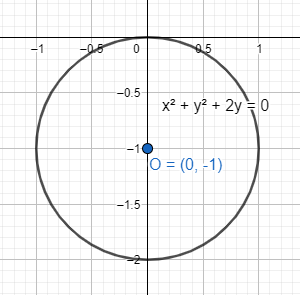
Note: In case of points for cartesian form we use x and y coordinates as $\left( x,y \right)$ to express their position in the cartesian plane. The distance from origin is $r=\sqrt{{{x}^{2}}+{{y}^{2}}}$. This r represents the distance in polar form.