Question

How do you graph \[y = 3{x^2} - 6x - 2\]?

Answer 1

Hint: We compare the given quadratic equation with general quadratic equation and write values of coefficients. Use the formula to calculate the value of vertex and substitute the values in it. Calculate coordinates of points to plot the graph by substituting different values of $x$.
The general quadratic equation is \[a{x^2} + bx + c = 0\]
Vertex \[(h,k)\] is given by the formula \[h = - \dfrac{b}{{2a}};k = f(h)\], where $f$ is the function given to us.
For a general quadratic equation \[a{x^2} + bx + c = 0\], roots are given by formula \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\]

Complete step by step answer:
We are given the equation \[y = 3{x^2} - 6x - 2\]
We compare the equation on right hand side to the general quadratic equation \[a{x^2} + bx + c = 0\]
We get the values \[a = 3,b = - 6,c = - 2\]
We know that vertex \[(h,k)\] is given by the formula \[h = - \dfrac{b}{{2a}};k = f(h)\], where f is the function given to us
Here function is \[y = 3{x^2} - 6x - 2\] … (1)
We substitute the values of ‘a’ and ‘b’ in formula of ‘h’
\[ \Rightarrow h = - \dfrac{{ - ( - 6)}}{{2 \times 3}}\]
\[ \Rightarrow h = - \dfrac{6}{6}\]
\[ \Rightarrow h = 1\]
Now we calculate the value of ‘k’ by substituting value of ‘h’ in place of ‘x’ in the function
\[ \Rightarrow k = f(1)\]
\[ \Rightarrow k = 3{(1)^2} - 6(1) - 2\]
\[ \Rightarrow k = 3 - 6 - 2\]
\[ \Rightarrow k = 3 - 8\]
\[ \Rightarrow k = - 5\]
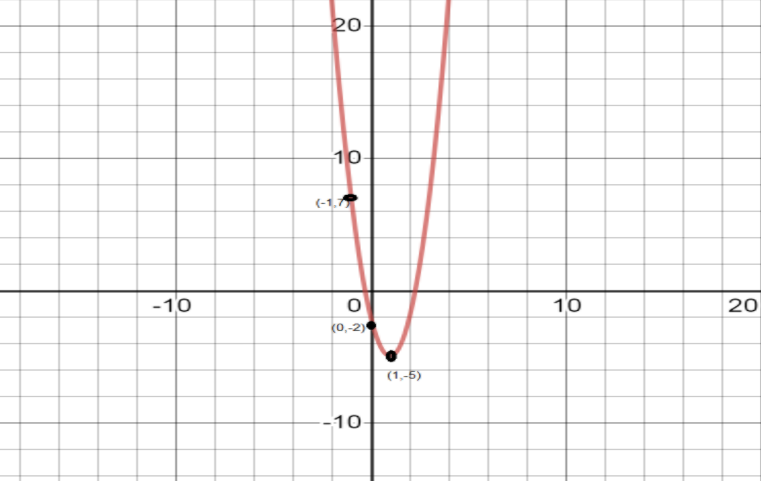
So, the vertex \[(h,k) = (1, - 5)\]
\[\therefore \] The vertex of \[y = 3{x^2} - 6x - 2\] is \[(1, - 5)\]
Now we plot the graph of the function \[y = 3{x^2} - 6x - 2\]by substituting points
We put \[x = 0\] in the equation, then \[y = - 2\]\[(0, - 2)\]
So, the point becomes \[(0, - 2)\]
Now we put \[x = 1\] in the equation, then \[y = 3{(1)^2} - 6(1) - 2\]i.e. \[y = - 5\]
So, the point becomes \[(1, - 5)\]
Now we put \[x = - 1\] in the equation, then \[y = 3{( - 1)^2} - 6( - 1) - 2\]i.e. \[y = 7\]
So, the point becomes \[( - 1,7)\]
We will mark the points, \[( - 1,7)\] and \[(1, - 5)\] on the graph. Also, we know that the equation in the question is equation of parabola as it is similar to general equation of parabola i.e. \[y = a{x^2} + bx + c\]

Note: Here $y$ is given in place of\[f(x)\], keep in mind the function is dependent on x and we will write the value of y as value of the function obtained by putting in the value of x. Also, whenever a quadratic equation is given, it must be an equation for the parabola as you need not have to plot all the points.