Question

How do you graph $y = - 4\tan x$?

Answer 1

Hint: We will write the given equation in the general format of the equation, and find the various parameters such as baseline, amplitude, and shift to plot the graph of the given equation.

Formula used: $y = a\tan (bx + c) + d$
Where $a$ is the amplitude of the equation which tells us the maximum and the minimum value the graph would go from the baseline value,
$b$ Is the period of the graph
$c$ Depicts the shift of the equation, positive shift represents that the graph is shifted towards the left and negative shift represents the graph shifting to right.
And $d$ is the baseline of the equation which tells us whether the graph is going upwards or downwards.

Complete step-by-step solution:
We have the given equation as:
 $y = - 4\tan x$, which is a cosine function which has amplitude$ - 4$.
 The period of the graph is $1$, since there is no coefficient present.
Since the value of $d$ is zero, we have the baseline in the graph as $0$.
Now the period of the function is found out as: $\dfrac{\pi }{b}$
Therefore, on substituting the value of $b$ as $1$, we get:
 $period = \dfrac{\pi }{1} = \pi $
On using the scientific calculator to calculate the value of $\pi $, we get:
$period \approx 3.142$
Therefore, the graph of the following function can be plotted as:

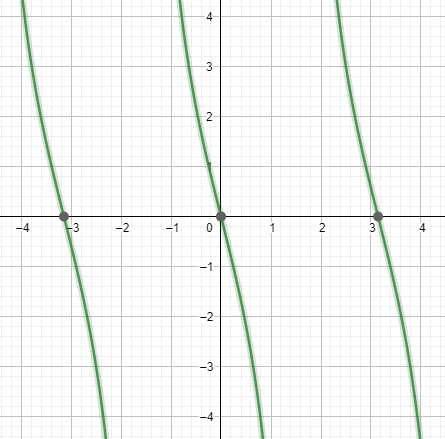
This is the required solution for the tangent function $y = - 4\tan x$

Note: In this question we are using the tangent function. There also exists the sine function and cosine function which is represented as: $y = a\sin (bx + c) + d$ and $y = a\cos (bx + c) + d$ , which have the same properties that of a tangent function.
The sign of the shift $c$ represents in which direction the shift is taking place, it could be negative or positive for right and left respectively.