Question

How do you graph \[y = 4x - 2\]?

Answer 1

Hint: To solve this we need to give the values of ‘x’ and we can find the values of ‘y’. Otherwise we can find the coordinate of the given equation lying on the line of x- axis, we can find this by substituting the value of ‘y’ is equal to zero (x-intercept). Similarly we can find the coordinate of the equation lying on the line of y- axis, we can find this by substituting the value of ‘x’ equal to zero (y-intercept).

Complete step-by-step solution:
Given, \[y = 4x - 2\].
To find the x-intercept. That is the value of ‘x’ at\[y = 0\]. Substituting this in the given equation. We have,
\[0 = 4x - 2\]
\[4x = 2\]
Divide by 4 on both sides,
\[x = \dfrac{2}{4}\]
\[x = \dfrac{1}{2}\]
\[x = 0.5\]
Thus we have a coordinate of the equation which lies on the line of x-axis. The coordinate is \[(0.5,0)\].
To find the y-intercept. That is the value of ‘y’ at \[x = 0\]. Substituting this in the given equation we have,
\[y = 4(0) - 2\]
\[y = - 2\].
Thus we have a coordinate of the equation which lies on the line of y-axis. The coordinate is \[(0, - 2)\].
Thus we have the coordinates \[(0.5,0)\] and \[(0, - 2)\]. This is enough to draw the graph.
Let’s plot a graph for this coordinates,
We take scale x-axis= 1 unit = 1 units; y-axis= 1 unit = 1 units

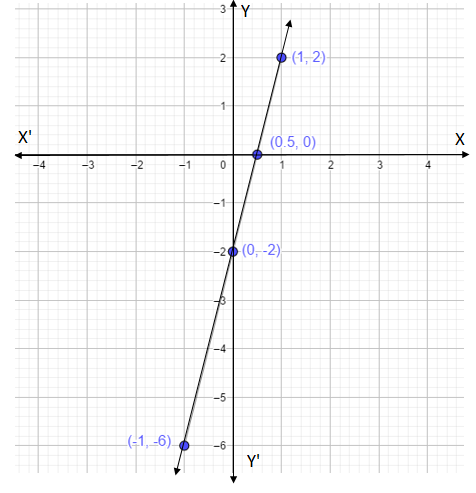
All we did was expand the line touching the coordinates \[(0.5,0)\] and \[(0, - 2)\] by a straight line.
Using the graph we have found out other coordinates that are \[( - 1, - 6),\] and \[(1,2)\]

Note: Intercept method is the easy and more accurate method to draw the graph of any equation. If the intercepts are zero then the given equation is passing through the origin and we find the coordinate points by giving the random values like 1, 2, 3,… to ‘x’ we find the corresponding value of ‘y’. Then with the obtained coordinate point we draw the graph ‘x’ versus ‘y’ as we did in above.