
How do you graph \[y = 5x - 2?\]
Answer
538.5k+ views
Hint: The given question describes the operation of addition/ subtraction/ multiplication/ division. Also, this problem involves substituting the \[x\] values in the given equation to find the value \[y\]. Also, \[y\] is the function of \[x\]. By using \[x\] and \[y\] values we can easily draw the graph for the given equation. We have to assume the value \[x\] for solving the given question.
Complete step by step solution:
The given equation is shown below,
\[y = 5x - 2 \to \left( 1 \right)\]
We would draw the graph for the above equation. As a first step, we would assume the \[x\] value as given below,
\[x = ....... - 2, - 1,0,1,2,.......\]
Let’s substitute \[x = - 2\] in the equation \[\left( 1 \right)\], we get
\[
\left( 1 \right) \to y = 5x - 2 \\
y = \left( {5 \times - 2} \right) - 2 \\
y = - 10 - 2 \\
y = - 12 \\
\]
Let’s substitute\[x = - 1\] in the equation \[\left( 1 \right)\], we get
\[
\left( 1 \right) \to y = 5x - 2 \\
y = \left( {5 \times - 1} \right) - 2 \\
y = - 5 - 2 \\
y = - 7 \\
\]
Let’s substitute \[x = 0\] in the equation \[\left( 1 \right)\], we get
\[
\left( 1 \right) \to y = 5x - 2 \\
y = \left( {5 \times 0} \right) - 2 \\
y = - 2 \\
\]
Let’s substitute \[x = 1\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = 5x - 2\]
\[
y = \left( {5 \times 1} \right) - 2 \\
y = 5 - 2 \\
y = 3 \\
\]
Let’s substitute \[x = 2\] in the equation \[\left( 1 \right)\], we get
\[
\left( 1 \right) \to y = 5x - 2 \\
y = \left( {5 \times 2} \right) - 2 \\
y = 10 - 2 \\
y = 8 \\
\]
Let’s make a tabular column by using the \[x\] and \[y\] values,
By using this table we can easily draw the following graph,
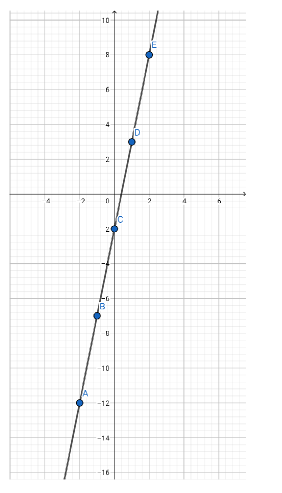
The above figure represents the equation \[y = 5x - 2\]
Note: This type of question involves the operation of addition/ subtraction/ multiplication/ division. In this type of question, we would assume the \[x\] value, by using the \[x\] value we can easily find the \[y\] values. Note that the graph would be based on the equation of \[y\]. \[y\] is the function of \[x\] so, \[y\] can also be written as \[f\left( x \right)\]. When multiplying the different sign numbers remember the following things,
1) When a negative number is multiplied with the negative number the answer becomes a
positive number
2) When a positive number is multiplied with the positive number the answer becomes a
positive number.
3) When a positive number is multiplied with the negative number the answer becomes a
negative number.
Complete step by step solution:
The given equation is shown below,
\[y = 5x - 2 \to \left( 1 \right)\]
We would draw the graph for the above equation. As a first step, we would assume the \[x\] value as given below,
\[x = ....... - 2, - 1,0,1,2,.......\]
Let’s substitute \[x = - 2\] in the equation \[\left( 1 \right)\], we get
\[
\left( 1 \right) \to y = 5x - 2 \\
y = \left( {5 \times - 2} \right) - 2 \\
y = - 10 - 2 \\
y = - 12 \\
\]
Let’s substitute\[x = - 1\] in the equation \[\left( 1 \right)\], we get
\[
\left( 1 \right) \to y = 5x - 2 \\
y = \left( {5 \times - 1} \right) - 2 \\
y = - 5 - 2 \\
y = - 7 \\
\]
Let’s substitute \[x = 0\] in the equation \[\left( 1 \right)\], we get
\[
\left( 1 \right) \to y = 5x - 2 \\
y = \left( {5 \times 0} \right) - 2 \\
y = - 2 \\
\]
Let’s substitute \[x = 1\] in the equation \[\left( 1 \right)\], we get
\[\left( 1 \right) \to y = 5x - 2\]
\[
y = \left( {5 \times 1} \right) - 2 \\
y = 5 - 2 \\
y = 3 \\
\]
Let’s substitute \[x = 2\] in the equation \[\left( 1 \right)\], we get
\[
\left( 1 \right) \to y = 5x - 2 \\
y = \left( {5 \times 2} \right) - 2 \\
y = 10 - 2 \\
y = 8 \\
\]
Let’s make a tabular column by using the \[x\] and \[y\] values,
| \[x\] | \[ - 2\] | \[ - 1\] | \[0\] | \[1\] | \[2\] |
| \[y\] | \[ - 12\] | \[ - 7\] | \[ - 2\] | \[3\] | \[8\] |
By using this table we can easily draw the following graph,

The above figure represents the equation \[y = 5x - 2\]
Note: This type of question involves the operation of addition/ subtraction/ multiplication/ division. In this type of question, we would assume the \[x\] value, by using the \[x\] value we can easily find the \[y\] values. Note that the graph would be based on the equation of \[y\]. \[y\] is the function of \[x\] so, \[y\] can also be written as \[f\left( x \right)\]. When multiplying the different sign numbers remember the following things,
1) When a negative number is multiplied with the negative number the answer becomes a
positive number
2) When a positive number is multiplied with the positive number the answer becomes a
positive number.
3) When a positive number is multiplied with the negative number the answer becomes a
negative number.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Differentiate between action potential and resting class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




