
How do you graph \[y = \cot x\]?
Answer
540k+ views
Hint: We need to graph the given function. We will use the domain and some values of \[x\] lying between \[ - 2\pi \] and \[2\pi \] to find some values of \[y\]. Then, we will observe the behavior of the value of \[y\], and use it and the coordinates obtained to graph the function.
Complete step-by-step solution:
The domain of the function \[y = \cot x\] is given by \[\left\{ {x:x \in R{\rm{ and }}x \ne n\pi ,n \in Z} \right\}\]. This means that the cotangent of any multiple of \[\pi \] does not exist.
The graph of the cotangent function reaches arbitrarily large positive or negative values at these multiples of \[\pi \].
Now, we will find some values of \[y\] for some values of \[x\] lying between \[ - 2\pi \] and \[2\pi \].
Substituting \[x = - \dfrac{{3\pi }}{2}\] in the function \[y = \cot x\], we get
\[\begin{array}{l}y = \cot \left( { - \dfrac{{3\pi }}{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Substituting \[x = - \dfrac{\pi }{2}\] in the function \[y = \cot x\], we get
\[\begin{array}{l}y = \cot \left( { - \dfrac{\pi }{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Substituting \[x = \dfrac{\pi }{2}\] in the function \[y = \cot x\], we get
\[\begin{array}{l}y = \cot \left( {\dfrac{\pi }{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Substituting \[x = \dfrac{{3\pi }}{2}\] in the function \[y = \cot x\], we get
\[\begin{array}{l}y = \cot \left( {\dfrac{{3\pi }}{2}} \right)\\ \Rightarrow y = 0\end{array}\]
The value of \[y\] at \[x = 2\pi ,\pi ,0,\pi ,2\pi \] is infinite.
Arranging the values of \[x\] and \[y\] in a table and writing the coordinates, we get
The value of \[y = \cot x\] decreases from \[\infty \] to 0 at \[x = - \dfrac{{3\pi }}{2}\], and then to \[ - \infty \] in the interval \[\left( { - 2\pi , - \pi } \right)\].
Similarly, the value of \[y = \cot x\] decreases from \[\infty \] to 0 at \[x = - \dfrac{\pi }{2},\dfrac{\pi }{2},\dfrac{{3\pi }}{2}\], and then to \[ - \infty \] in the intervals \[\left( { - \pi ,0} \right)\], \[\left( {0,\pi } \right)\], and \[\left( {\pi ,2\pi } \right)\].
Now, we will use the points \[\left( { - \dfrac{{3\pi }}{2},0} \right)\], \[\left( { - \dfrac{\pi }{2},0} \right)\], \[\left( {\dfrac{\pi }{2},0} \right)\], \[\left( {\dfrac{{3\pi }}{2},0} \right)\] and the behaviour of the value of \[y = \cot x\] to graph the function.
Therefore, we get the graph
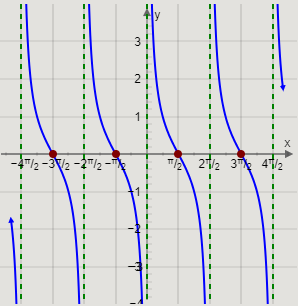
This is the required graph of the function \[y = \cot x\].
Note:
The period of the function \[y = \cot x\] is \[\pi \]. This means that the graph of \[y = \cot x\] will repeat for every \[\pi \] distance on the \[x\]-axis. It can be observed that the pattern and shape of the graph of \[y = \cot x\] is the same from \[ - 2\pi \] to \[ - \pi \], from \[ - \pi \] to 0, from 0 to \[\pi \], and from \[\pi \] to \[2\pi \]. The range of cotangent functions is from \[ - \infty \] to \[\infty \]. As tangent function is a reciprocal function cotangent function, so their graph faces opposite to each other.
Complete step-by-step solution:
The domain of the function \[y = \cot x\] is given by \[\left\{ {x:x \in R{\rm{ and }}x \ne n\pi ,n \in Z} \right\}\]. This means that the cotangent of any multiple of \[\pi \] does not exist.
The graph of the cotangent function reaches arbitrarily large positive or negative values at these multiples of \[\pi \].
Now, we will find some values of \[y\] for some values of \[x\] lying between \[ - 2\pi \] and \[2\pi \].
Substituting \[x = - \dfrac{{3\pi }}{2}\] in the function \[y = \cot x\], we get
\[\begin{array}{l}y = \cot \left( { - \dfrac{{3\pi }}{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Substituting \[x = - \dfrac{\pi }{2}\] in the function \[y = \cot x\], we get
\[\begin{array}{l}y = \cot \left( { - \dfrac{\pi }{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Substituting \[x = \dfrac{\pi }{2}\] in the function \[y = \cot x\], we get
\[\begin{array}{l}y = \cot \left( {\dfrac{\pi }{2}} \right)\\ \Rightarrow y = 0\end{array}\]
Substituting \[x = \dfrac{{3\pi }}{2}\] in the function \[y = \cot x\], we get
\[\begin{array}{l}y = \cot \left( {\dfrac{{3\pi }}{2}} \right)\\ \Rightarrow y = 0\end{array}\]
The value of \[y\] at \[x = 2\pi ,\pi ,0,\pi ,2\pi \] is infinite.
Arranging the values of \[x\] and \[y\] in a table and writing the coordinates, we get
| \[x\] | \[y\] |
| \[ - 2\pi \] | \[\infty \] |
| \[ - \dfrac{{3\pi }}{2}\] | \[0\] |
| \[ - \pi \] | \[\infty \] |
| \[ - \dfrac{\pi }{2}\] | \[0\] |
| \[0\] | \[\infty \] |
| \[\dfrac{\pi }{2}\] | \[0\] |
| \[\pi \] | \[\infty \] |
| \[\dfrac{{3\pi }}{2}\] | \[0\] |
| \[2\pi \] | \[\infty \] |
The value of \[y = \cot x\] decreases from \[\infty \] to 0 at \[x = - \dfrac{{3\pi }}{2}\], and then to \[ - \infty \] in the interval \[\left( { - 2\pi , - \pi } \right)\].
Similarly, the value of \[y = \cot x\] decreases from \[\infty \] to 0 at \[x = - \dfrac{\pi }{2},\dfrac{\pi }{2},\dfrac{{3\pi }}{2}\], and then to \[ - \infty \] in the intervals \[\left( { - \pi ,0} \right)\], \[\left( {0,\pi } \right)\], and \[\left( {\pi ,2\pi } \right)\].
Now, we will use the points \[\left( { - \dfrac{{3\pi }}{2},0} \right)\], \[\left( { - \dfrac{\pi }{2},0} \right)\], \[\left( {\dfrac{\pi }{2},0} \right)\], \[\left( {\dfrac{{3\pi }}{2},0} \right)\] and the behaviour of the value of \[y = \cot x\] to graph the function.
Therefore, we get the graph

This is the required graph of the function \[y = \cot x\].
Note:
The period of the function \[y = \cot x\] is \[\pi \]. This means that the graph of \[y = \cot x\] will repeat for every \[\pi \] distance on the \[x\]-axis. It can be observed that the pattern and shape of the graph of \[y = \cot x\] is the same from \[ - 2\pi \] to \[ - \pi \], from \[ - \pi \] to 0, from 0 to \[\pi \], and from \[\pi \] to \[2\pi \]. The range of cotangent functions is from \[ - \infty \] to \[\infty \]. As tangent function is a reciprocal function cotangent function, so their graph faces opposite to each other.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




