
How do you graph
Answer
450.6k+ views
Hint: From the given question we have been asked to find the graph of the logarithmic function
Complete step by step answer:
Firstly, as we said before we will start by finding the first derivative of the function
Here we use the product rule of differentiation which is
Now, we can see that this will give us the graph of
Now, we will find the critical numbers, which will occur or we can find them when the derivative is equated to zero or is undefined.
The derivative will be undefined whenever
So, now when we equate the derivative to zero, we get,
Now we will remove the logarithm. So, we get,
Now, we will check on both sides of this point.
Test point:
This is negative.
Test point:
This is positive.
Therefore,
Now, we will find the second derivative.
Here we use the formula
If we set this to zero to find the points of inflection, we find,
This is a contradiction, so there are no points of inflection.
Finally, we analyze the intercepts.
There will be no y-intercept because
But the initial function
So, the graph will be as follows.
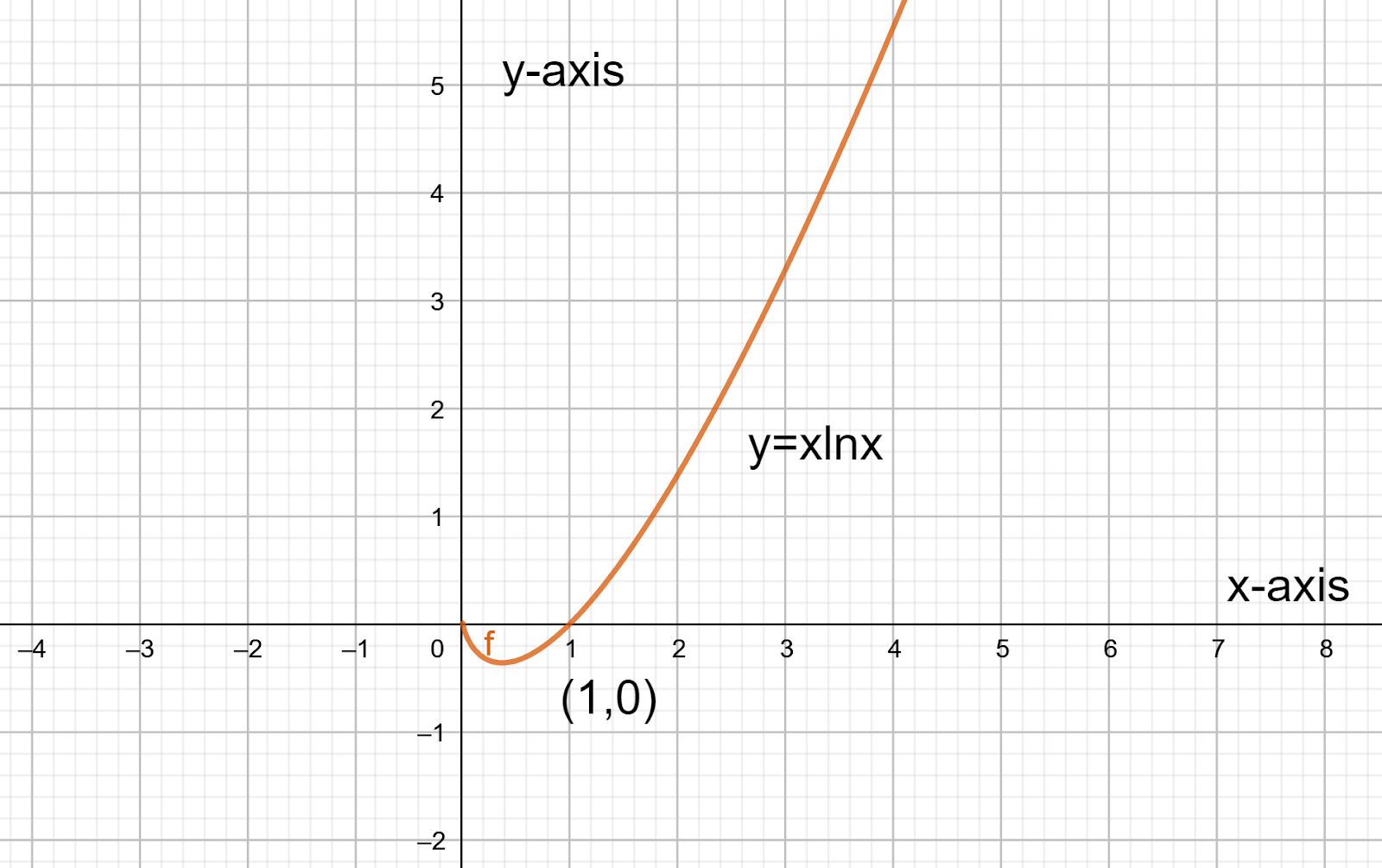
Note: Students must have good knowledge in the concept of differentiation and its applications. Students must not make any calculation mistakes. Students should know the basic differentiation formulae like,
The product rule or UV rule,
And also the formula for logarithmic function which is as follows.
Complete step by step answer:
Firstly, as we said before we will start by finding the first derivative of the function
Here we use the product rule of differentiation which is
Now, we can see that this will give us the graph of
Now, we will find the critical numbers, which will occur or we can find them when the derivative is equated to zero or is undefined.
The derivative will be undefined whenever
So, now when we equate the derivative to zero, we get,
Now we will remove the logarithm. So, we get,
Now, we will check on both sides of this point.
Test point:
This is negative.
Test point:
This is positive.
Therefore,
Now, we will find the second derivative.
Here we use the formula
If we set this to zero to find the points of inflection, we find,
This is a contradiction, so there are no points of inflection.
Finally, we analyze the intercepts.
There will be no y-intercept because
But the initial function
So, the graph will be as follows.
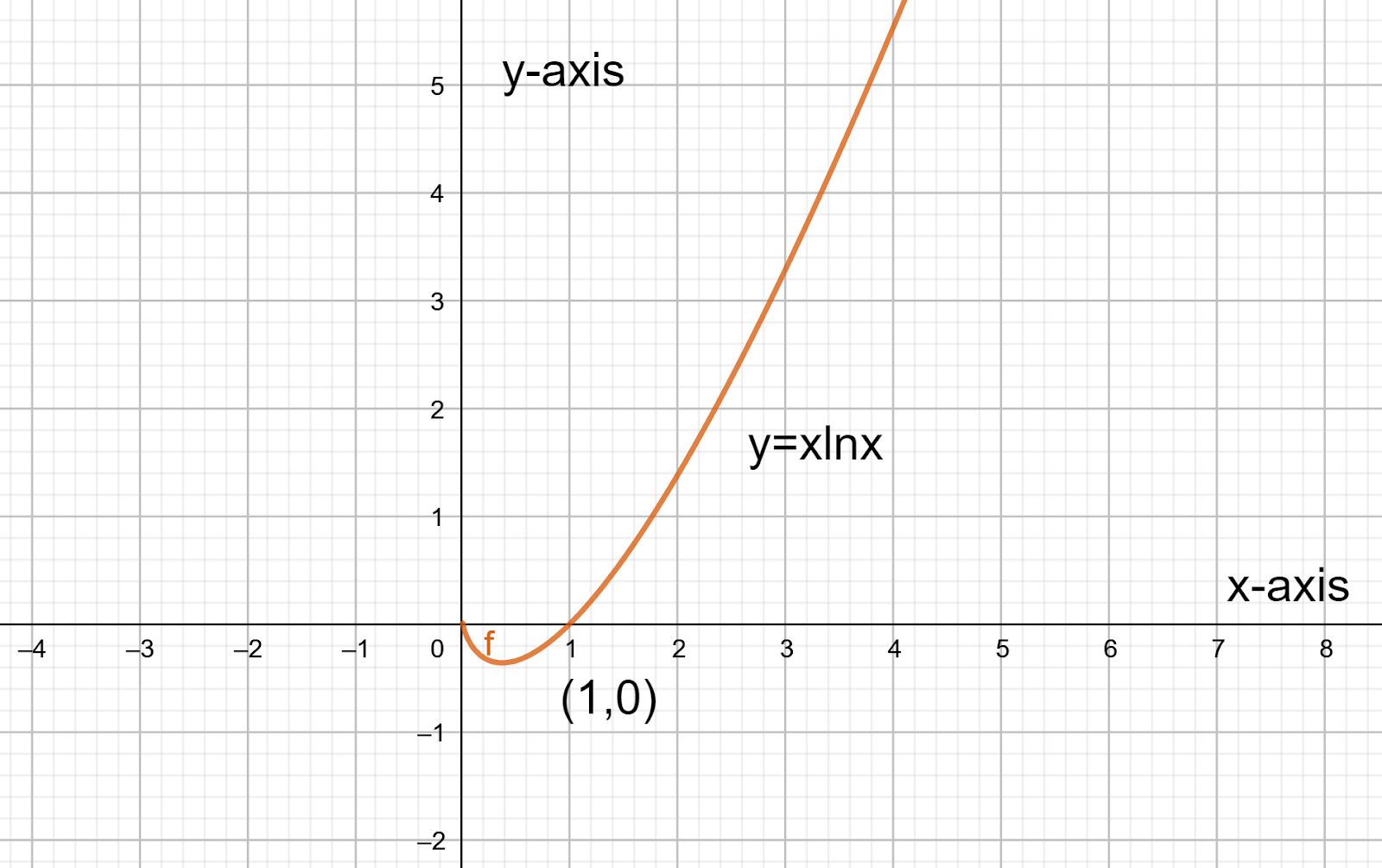
Note: Students must have good knowledge in the concept of differentiation and its applications. Students must not make any calculation mistakes. Students should know the basic differentiation formulae like,
The product rule or UV rule,
And also the formula for logarithmic function which is as follows.
Latest Vedantu courses for you
Grade 8 | CBSE | SCHOOL | English
Vedantu 8 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
EMI starts from ₹3,775 per month
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Draw a diagram of a flower and name the parts class 12 biology ICSE




