Question

How do you solve $10={{e}^{x}}$ ?

Answer 1

Hint: We treat the two sides of the equation as two separate equations. Thus, we get two equations, which are $y={{e}^{x}}$ and $y=10$. We plot these two equations on a graph paper and find out the point of intersection which is the required solution.

Complete step-by-step solution:
The given equation is
$10={{e}^{x}}$
We solve the problem using the graphical method that is by using graphs. We treat the two sides of the equation as two separate equations. Thus, we get two equations, which are
$y={{e}^{x}}$ and $y=10$
We plot the two above equations on a single graph paper. Now, these two equations are two separate and completely different types of equations, and their respective graphs will be different. One is an exponential graph and the other is a straight line. If two different graphs intersect at some point, then that point is the common point for both the graphs. This means that the point of intersection is such a point which satisfies both the equations of the different graphs. The abscissa of the point of intersection will be the solution to the equations of the graphs which are in this case, $y={{e}^{x}}$ and $y=10$ .
The number of solutions to two functions will be the number of points of intersection of the two functions. If the number of points of intersection is one, then the number of solutions is one, if the number of points of intersection is zero, then there are no solutions and so on.

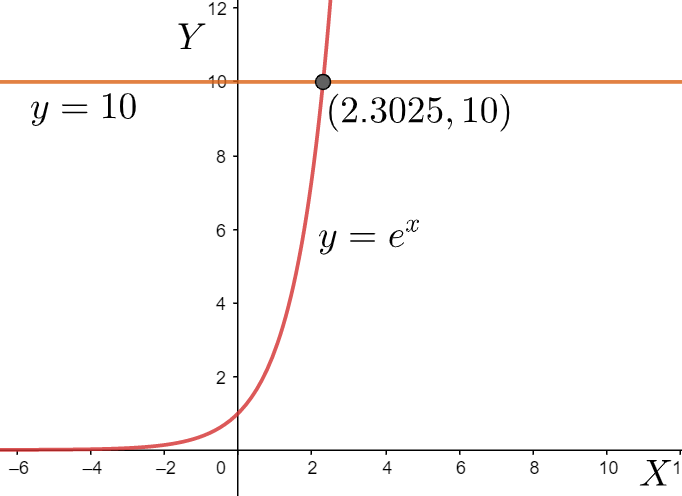
In the above graph, it is seen that the two graphs meet at the point $\left( 2.3025,10 \right)$ . This is the only point of intersection.
Therefore, we can conclude that the solution of the given equation $10={{e}^{x}}$ is $2.3025$ .

Note: We should plot the respective graphs carefully. We should look for more than one point of intersection if there. This problem can also be solved by taking natural logarithms on both sides.
$\begin{align}
  & \Rightarrow \ln 10=\ln \left( {{e}^{x}} \right) \\
 & \Rightarrow \ln 10=x\ln e \\
 & \Rightarrow x=\dfrac{\ln 10}{\ln e} \\
 & \Rightarrow x=2.3025 \\
\end{align}$