
How do you solve and graph $ - x - 4y > 3?$
Answer
526.8k+ views
Hint: To solve inequality consider it as normal equation and solve for its points by putting random values of independent variable to get value of dependent variable and collecting some points, draw its graph as a normal graph should be drawn and then check for any point on the graph (not the point on line) and if it satisfies the inequality then shade whole portion on which the point lies and also if inequality is not saying equals to then draw the dotted graph of the equation.
Complete step by step solution:
In order to solve and graph the given inequality $ - x - 4y > 3$, we will first simplify this inequality by making the coefficients of variables positive as follows
$
\Rightarrow - x - 4y > 3 \\
\Rightarrow - (x + 4y) > 3 \\
$
Multiplying both sides with $ - 1$, we will get
$
\Rightarrow - 1 \times - (x + 4y) < - 1 \times 3 \\
\Rightarrow x + 4y < - 3 \\
$
Now considering it as a normal equation by removing the inequality sign, in order to find the points to plot the respective graph
$ \Rightarrow x + 4y = - 3$
We can write it as
$ \Rightarrow y = \dfrac{{ - 3 - x}}{4}$
Collecting coordinate of points in the table below:
So, we got some points $(1,\; - 1),\;( - 3,\;0),\;(5,\; - 2)$ plotting these points on a graph and making a line from it, as follows
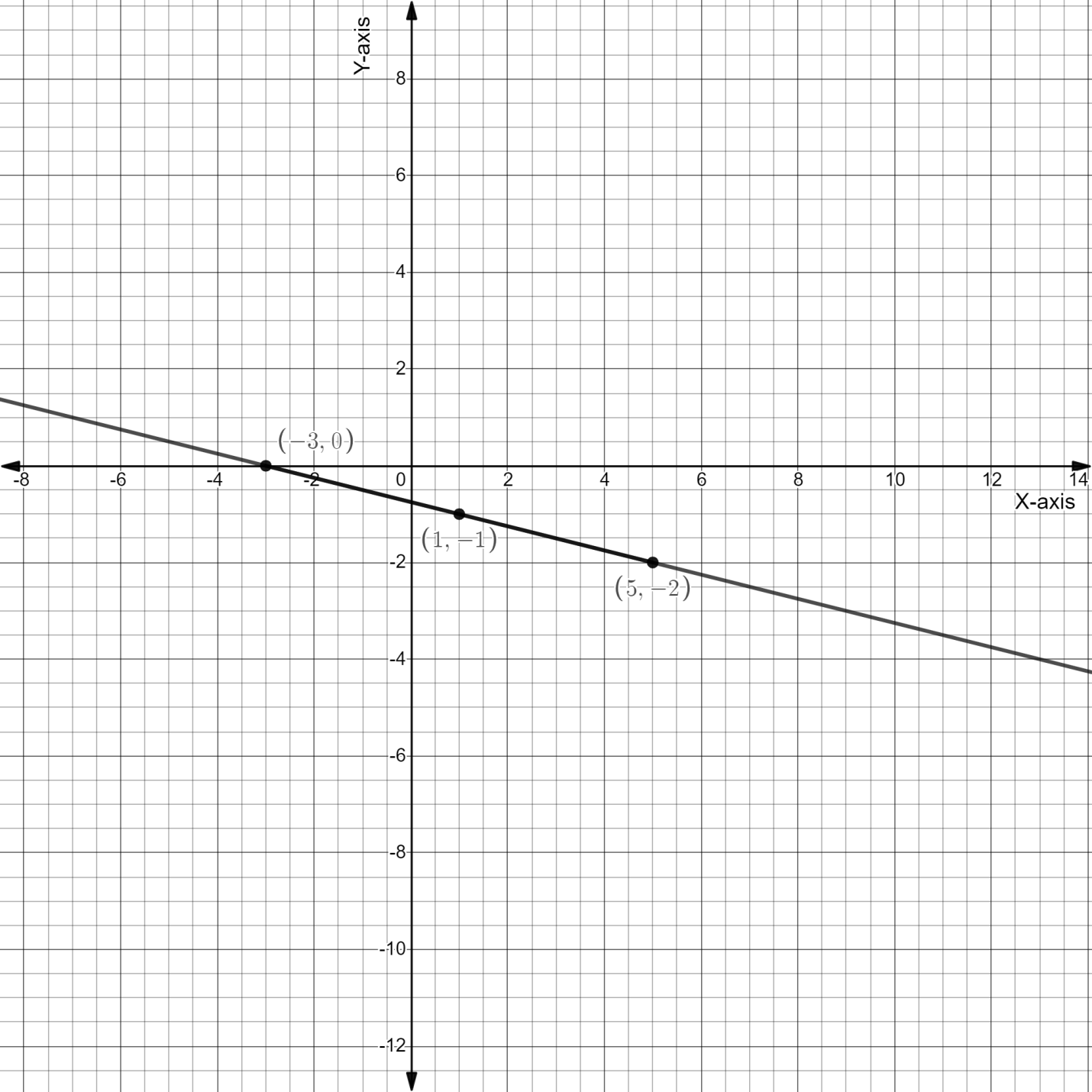
Now coming to the inequality,
$ \Rightarrow x + 4y < - 3$
And checking if $(0,\;0)$ is satisfying it or not,
$
\Rightarrow 0 + 4 \times 0 < - 3 \\
\Rightarrow 0 < - 3 \\
$
Since $(0,\;0)$ do not hold good for the given inequation, therefore we will shade portion opposite to $(0,\;0)$ and also since the inequality says less than not less than equals to, so we will draw dotted line
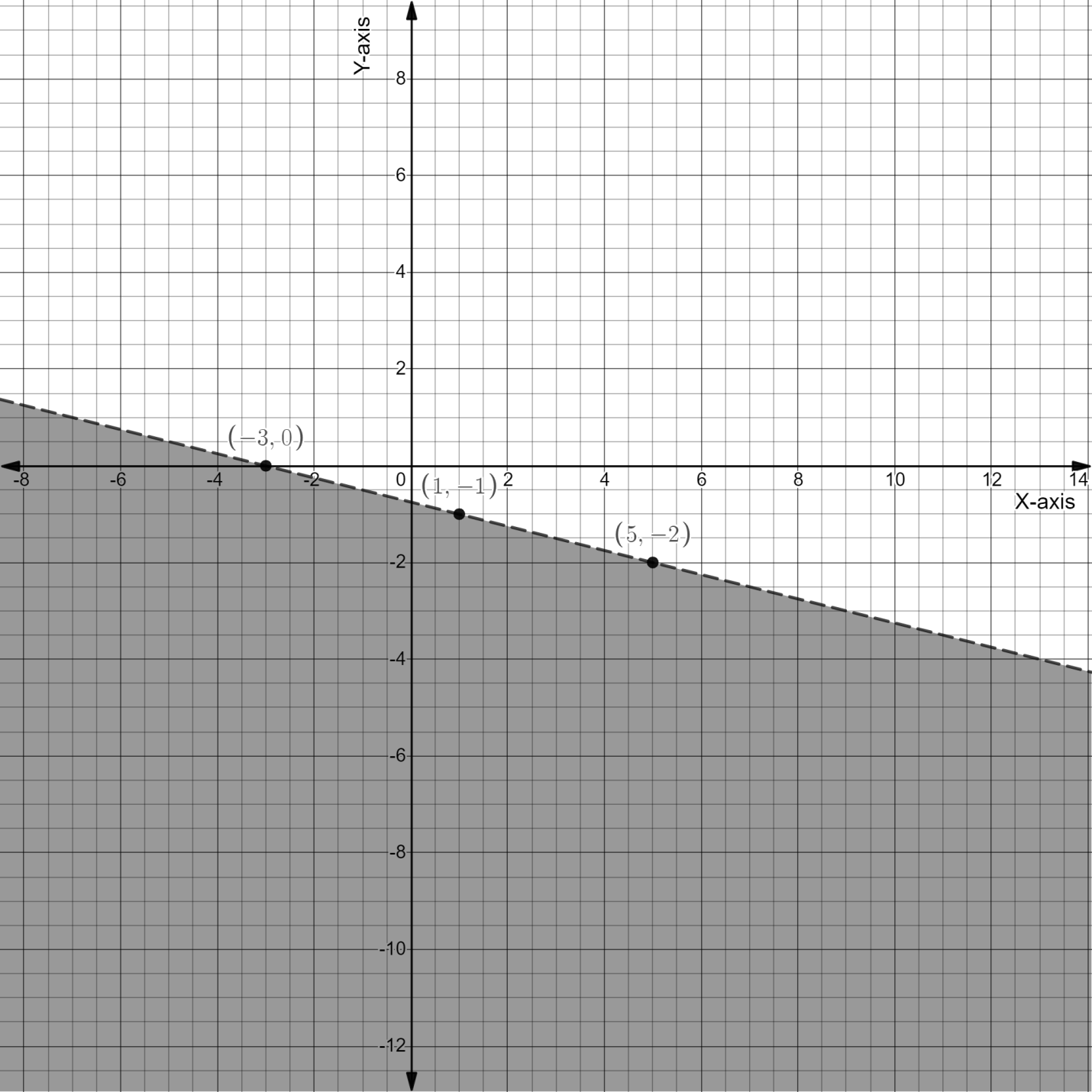
This is the required graph for the inequality.
Note: Inequality sign inverted when we have multiplied $ - 1$ to the equation, let us understand it with example the inequality $2 < 3$ but when we multiply it with $ - 1$ that is $ - 1 \times 2 > - 1 \times 3 \Rightarrow - 2 > - 3$ the inequality changes.
Complete step by step solution:
In order to solve and graph the given inequality $ - x - 4y > 3$, we will first simplify this inequality by making the coefficients of variables positive as follows
$
\Rightarrow - x - 4y > 3 \\
\Rightarrow - (x + 4y) > 3 \\
$
Multiplying both sides with $ - 1$, we will get
$
\Rightarrow - 1 \times - (x + 4y) < - 1 \times 3 \\
\Rightarrow x + 4y < - 3 \\
$
Now considering it as a normal equation by removing the inequality sign, in order to find the points to plot the respective graph
$ \Rightarrow x + 4y = - 3$
We can write it as
$ \Rightarrow y = \dfrac{{ - 3 - x}}{4}$
Collecting coordinate of points in the table below:
| $x$ | $y = \dfrac{{ - 3 - x}}{4}$ | Coordinate $(x,\;y)$ |
| $1$ | $ - 1$ | $(1,\; - 1)$ |
| $ - 3$ | $0$ | $( - 3,\;0)$ |
| $5$ | $ - 2$ | $(5,\; - 2)$ |
So, we got some points $(1,\; - 1),\;( - 3,\;0),\;(5,\; - 2)$ plotting these points on a graph and making a line from it, as follows

Now coming to the inequality,
$ \Rightarrow x + 4y < - 3$
And checking if $(0,\;0)$ is satisfying it or not,
$
\Rightarrow 0 + 4 \times 0 < - 3 \\
\Rightarrow 0 < - 3 \\
$
Since $(0,\;0)$ do not hold good for the given inequation, therefore we will shade portion opposite to $(0,\;0)$ and also since the inequality says less than not less than equals to, so we will draw dotted line

This is the required graph for the inequality.
Note: Inequality sign inverted when we have multiplied $ - 1$ to the equation, let us understand it with example the inequality $2 < 3$ but when we multiply it with $ - 1$ that is $ - 1 \times 2 > - 1 \times 3 \Rightarrow - 2 > - 3$ the inequality changes.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




