Answer
463.8k+ views
Hint: In this question, we are given that A, B and C are three points on a line, and B lies between A and C. As, we know that two segments will be equal if the coordinates of their end points are equal, we should try to find out the coordinates of the endpoints of AB+BC and AC and show that the coordinates are equal.
Complete step by step solution:
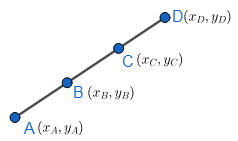
Let the following figure represent the situation geometrically. Now, let the coordinates of A be $\left( {{x}_{A}},{{y}_{A}} \right)$, that of B be \[\left( {{x}_{B}},{{y}_{B}} \right)\] , C be \[\left( {{x}_{C}},{{y}_{C}} \right)\] and that of D be \[\left( {{x}_{D}},{{y}_{D}} \right)\] …………………………(1.1)
Also, we know that when we add two line segments having one common endpoint, the coordinates of the resulting lines should be the coordinates of the points other than the common point, eg. Coordinates of endpoints upon addition of two segments PQ and QR where Q is the common point should be given by the coordinates of P and Q………………………………………..(1.2)
Therefore, (1.1) and (1.2), as B is the common endpoint, the starting point of AB+BC should be at A and the coordinates of other endpoint of AB+BC should the coordinates of C……………………(1.3)
Also, we know that two line segments are said to be equal if the coordinates of their end points are equal. Therefore, as A and C are the coordinates of end points of AC and from (1.3), as these coordinates match the coordinates of the endpoints of AB+BC, we can write AB+BC=AC which is the equation asked to be proved.
Note: We should note that we could use equation (1.2) in equation (1.3) only because B was a common end point between AB and BC. However, if there was no common endpoint then we could not have used the formula. However, the formula can still be used if AB and BC are given to be vectors, as vectors can be translated in parallel to match one end point of the two segments and thus we can then use (1.2) in that case.
Complete step by step solution:
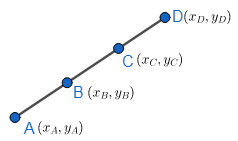
Let the following figure represent the situation geometrically. Now, let the coordinates of A be $\left( {{x}_{A}},{{y}_{A}} \right)$, that of B be \[\left( {{x}_{B}},{{y}_{B}} \right)\] , C be \[\left( {{x}_{C}},{{y}_{C}} \right)\] and that of D be \[\left( {{x}_{D}},{{y}_{D}} \right)\] …………………………(1.1)

Also, we know that when we add two line segments having one common endpoint, the coordinates of the resulting lines should be the coordinates of the points other than the common point, eg. Coordinates of endpoints upon addition of two segments PQ and QR where Q is the common point should be given by the coordinates of P and Q………………………………………..(1.2)
Therefore, (1.1) and (1.2), as B is the common endpoint, the starting point of AB+BC should be at A and the coordinates of other endpoint of AB+BC should the coordinates of C……………………(1.3)
Also, we know that two line segments are said to be equal if the coordinates of their end points are equal. Therefore, as A and C are the coordinates of end points of AC and from (1.3), as these coordinates match the coordinates of the endpoints of AB+BC, we can write AB+BC=AC which is the equation asked to be proved.
Note: We should note that we could use equation (1.2) in equation (1.3) only because B was a common end point between AB and BC. However, if there was no common endpoint then we could not have used the formula. However, the formula can still be used if AB and BC are given to be vectors, as vectors can be translated in parallel to match one end point of the two segments and thus we can then use (1.2) in that case.
Recently Updated Pages
Who among the following was the religious guru of class 7 social science CBSE

what is the correct chronological order of the following class 10 social science CBSE

Which of the following was not the actual cause for class 10 social science CBSE

Which of the following statements is not correct A class 10 social science CBSE

Which of the following leaders was not present in the class 10 social science CBSE

Garampani Sanctuary is located at A Diphu Assam B Gangtok class 10 social science CBSE

Trending doubts
Derive an expression for drift velocity of free electrons class 12 physics CBSE

Which are the Top 10 Largest Countries of the World?

Write down 5 differences between Ntype and Ptype s class 11 physics CBSE

The energy of a charged conductor is given by the expression class 12 physics CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Derive an expression for electric field intensity due class 12 physics CBSE

How do you graph the function fx 4x class 9 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Derive an expression for electric potential at point class 12 physics CBSE