Question

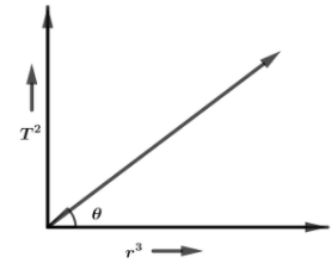
If a graph is plotted between ${T^2}$ and ${r^3}$ for a planet, then its slope will be

A. $\dfrac{{4{\pi ^2}}}{{GM}}$
B. $\dfrac{{GM}}{{4{\pi ^2}}}$
C. $4\pi GM$
D. $zero$

Answer 1

Hint:We can solve this problem by using Kepler’s third law of planetary motion. And then we will solve for its third law equation and then by rearranging different parameters we will find the value for $\dfrac{{{T^2}}}{{{r^3}}}$ which will be the value of slope of the curve given in the question.

Complete step by step answer:
There are major three laws of planetary motion given by kepler. The First law states that “Planetary orbits are elliptical with the sun at a focus”. The Second law states that “The radius vector from the sun to a planet sweeps equal areas in equal times”.

The third which is most important law states that “The ratio of square of the period of revolution of a planet and the cube of the semi major axis of ellipse is a constant for all planets.Now, we know the time period of a planet is given by
$T = \dfrac{{2\pi {r^{\dfrac{3}{2}}}}}{{\sqrt {GM} }}$
Where $T$ is time period, $r$ is a semi major axis and $M$ Is the mass of the sun and $G$ is the Gravitational constant.
Squaring above equation on both side we get,
${T^2} = \dfrac{{4{\pi ^2}{r^3}}}{{GM}}$
Now, we will take the ration of time period and semi major axis which is the slope of the line
Slope of line $\dfrac{{{T^2}}}{{{r^3}}} = \dfrac{{4{\pi ^2}}}{{GM}}$

Hence, the correct option is A.

Note:A planet always moves in an elliptical path with the sun at its one focus and the distance measured from the sun to the planet is generally taken as the semi major axis while applying in Kepler’s third law. Kepler’s third law is very useful when we need to find the time period of a planet when we know only its distance from the sun.