Question

If a hexagon ABCDEF circumscribe a circle, prove that \[\text{AB}+\text{CD}+\text{EF}=\text{BC}+\text{DE}+\text{FA}\].

Answer 1

Hint: We are given a hexagon ABCDEF, we are asked to show \[\text{AB}+\text{CD}+\text{EF}=\text{BC}+\text{DE}+\text{FA}\]. To do so, we use that the tangent drawn from the same external point is equal in length. We got 6 tangents on the circle touching the hexagon at 6 points, we then took the right hand side BC + DE + FA then split the side and used the tangent part to get our required solution.

Complete step by step answer:
We are given a hexagon ABCDEF that circumscribes a circle, we know circumscribing a circle means the hexagon contains a circle which touches all its edges at some point. Let circle touch hexagon at L, M, N, O, P and Q. So,

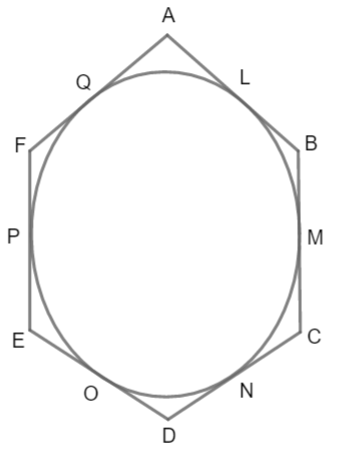
Now we know, a pair of tangents coming from the same external point to a circle are equal in length.
Now, for the circle AQ and AL are tangent that is from same point A. So,
\[AQ=AL\cdots \cdots \cdots \cdots \cdots \cdots \left( 1 \right)\]
Similarly, FQ and FP are the tangent to the circle from the same external point F. So,
\[FQ=FP\cdots \cdots \cdots \cdots \cdots \cdots \left( 2 \right)\]
Now, also EP and EO are tangent from same external point E. So,
\[EO=EP\cdots \cdots \cdots \cdots \cdots \cdots \left( 3 \right)\]
Also, we have DO and DN are tangent to circle from external same point D. So,
\[DO=DN\cdots \cdots \cdots \cdots \cdots \cdots \left( 4 \right)\]
Now, NC and MC are tangent to circle from same external point C. So,
\[MC=NC\cdots \cdots \cdots \cdots \cdots \cdots \left( 5 \right)\]
Lastly, BL and BM are tangent to circle from same external point B. So,
\[BM=BL\cdots \cdots \cdots \cdots \cdots \cdots \left( 6 \right)\]
Now, we are asked to show \[\text{AB}+\text{CD}+\text{EF}=\text{BC}+\text{DE}+\text{FA}\]
We consider right hand side $BC+DE+FA$ we can see from figure, we can split side of hexagon as
\[BC+DE+FA=\left( BM+MC \right)+\left( DO+EO \right)+\left( FQ+QA \right)\]
Now using (1), (2), (3), (4), (5) and (6) we get:
\[\Rightarrow \left( BL+NC \right)+\left( DN+EP \right)+\left( AL+FP \right)\]
Now, we arrange the terms, so we get:
\[\Rightarrow \left( BL+AL \right)+\left( NC+DN \right)+\left( EP+FP \right)\]
Now, $\left( BL+AL=AB \right),\left( NC+DN=CD \right)\text{ and }\left( EP+FP=EF \right)$ so we get:
\[\begin{align}
  & \Rightarrow AB+CD+EF \\
 & \Rightarrow LHS \\
\end{align}\]
Hence proved.

Note:
While writing the equal tangent then at that time we put part by part in sequential order. Remember, if there is a point saying non straight line AB then we can always write AB = AX + XB. This is the property of collinearity for the straight line as the hexagon has straight sides, so we use this there.