Question

If \[A \subset B\] then show that \[A \cap B = {\rm A}\] (Use Venn Diagram).

Answer 1

Hint:In the above given question, we are given two sets A and B respectively. It is also given the condition that the Set A is a subset of the Set B i.e. \[A \subset B\] . Using this information, we have to show that the complement of the two sets A and B, is actually equal to the smaller set i.e. Set A. In order to approach the solution, we can use the method of Venn Diagrams to support our answer.

Complete step by step answer:
Given condition is that Set A is the subset of Set B, that can be written as,
\[ \Rightarrow A \subset B\]
Clearly, this condition states that Set B is bigger than the first Set A.Hence, the larger Set B also contains the smaller Set A.

Now, using the Venn Diagram, we can show this situation by drawing a bigger circle representing Set B , which contains a smaller circle representing Set A. Hence, the required Venn Diagram of the given Set A and Set B can be drawn as the diagram given below.

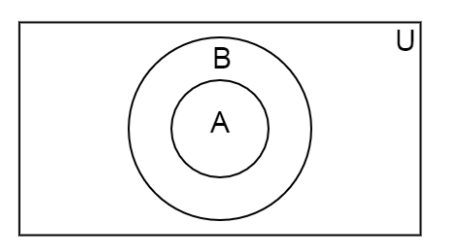
Here in the above diagram, the rectangle U represents the universal set. Now, we have to show that \[A \cap B = {\rm A}\]. The complement of two sets is the common part of those two sets that they share with each other.Hence, from the Venn Diagram, we can see that the common part between the circle A and circle B is the smaller circle A itself.Therefore, the complement of Set A and Set B is the smaller Set A.Therefore, we can write
\[ \Rightarrow A \cap B = {\rm A}\]
Hence proved.

Note:The symbol \[ \cap \] stands for the compliment between two sets which is the common part between the given two sets. Whereas the symbol \[ \cup \] stands for the union of two sets which is the total combined part of the two sets that they share together.Also if, \[A \subset B\] then similarly we have \[A \cup B = B\].