
If C is the midpoint of AB and P is any point outside AB then,
(a)
(b)
(c)
(d)
Answer
496.2k+ views
Hint: In order to solve this problem, we need to carefully draw the vector diagram. From the vector diagram, we need to find the relation of the
Complete ste-by-step solution:
In this question, we are given that the point C is the midpoint of line AB.
Let there be the point P outside the line AB.
Let's draw and understand the figure better.
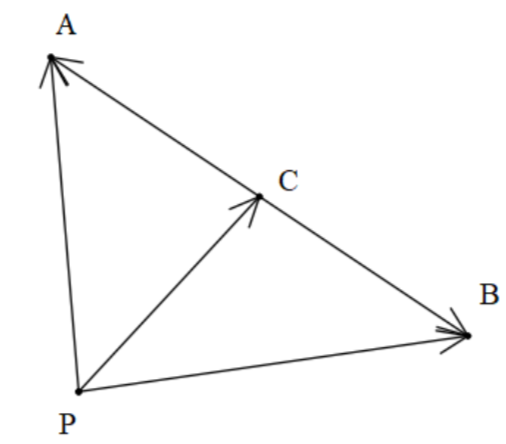
As we can see that point C is the midpoint of line AB.
The vector can be expressed as starting from the tail to the tip.
For example, for vector
In the triangle, ACP, we can write as follows,
We can say this as we can go from P to A directly from P to A vector or we can go to C and then from C to A.
Similarly, in triangle PCB, we can write as follows,
We can say this as we can go from P to B directly from P to B vector or we can go to C and then from C to B.
Adding two equation we get,
Solving this we can say that,
The vector
Hence, the distance from point C to A and from C to B is the same.
So, we can write as,
Substituting we get,
Hence, the correct option is (b).
Note:In this question, the direction of the vector is very important. From which point we consider the tail and from which we consider the tail is important. For a hint, we can check what all vectors are present from the option given below. Also, we need to be careful while adding the two vectors with the tail of the first vector, and the head of the second vector can be added together, and the resultant of these vectors from the head of the first vector to the tail of the second vector.
Complete ste-by-step solution:
In this question, we are given that the point C is the midpoint of line AB.
Let there be the point P outside the line AB.
Let's draw and understand the figure better.

As we can see that point C is the midpoint of line AB.
The vector can be expressed as starting from the tail to the tip.
For example, for vector
In the triangle, ACP, we can write as follows,
We can say this as we can go from P to A directly from P to A vector or we can go to C and then from C to A.
Similarly, in triangle PCB, we can write as follows,
We can say this as we can go from P to B directly from P to B vector or we can go to C and then from C to B.
Adding two equation we get,
Solving this we can say that,
The vector
Hence, the distance from point C to A and from C to B is the same.
So, we can write as,
Substituting we get,
Hence, the correct option is (b).
Note:In this question, the direction of the vector is very important. From which point we consider the tail and from which we consider the tail is important. For a hint, we can check what all vectors are present from the option given below. Also, we need to be careful while adding the two vectors with the tail of the first vector, and the head of the second vector can be added together, and the resultant of these vectors from the head of the first vector to the tail of the second vector.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Why is the cell called the structural and functional class 12 biology CBSE




