Question

If $ f(x) $ is a twice differentiable function such that $ f(a)=0,f(b)=2,f(c)=1,f(d)=2,f(e)=0 $ , where a < b < c < d < e , then the minimum number of zeroes of $ g(x)={{\left( f'(x) \right)}^{2}}+f''(x)f(x) $ in the interval [a,e] is:

Answer 1

Hint: As we are asked about the number of zeroes of g(x), we will take $ {{\left( f'(x) \right)}^{2}}+f''(x)f(x)=0 $ and if you have noticed that $ {{\left( f'(x) \right)}^{2}}+f''(x)f(x)=\dfrac{d\left( f(x)f'(x) \right)}{dx} $ . So, we will let $ f(x)f'(x)=h(x) $. Now if h(x) is 0, h’(x) is surely zero, so we will find the number of points where h(x) is zero to get the answer. You need to use a representative graph of f(x) and use the property that f’(x) is zero at the points where f(x) has a turn, i.e., at local maxima or minima. Also, use the property that if a function is zero at n points then its derivative will have at least n-1 zeroes.

Complete step-by-step answer:
Let us start with the solution to the above question. : As we are asked about the number of zeroes of g(x), we will take $ {{\left( f'(x) \right)}^{2}}+f''(x)f(x)=0 $ and if you have noticed that $ {{\left( f'(x) \right)}^{2}}+f''(x)f(x)=\dfrac{d\left( f(x)f'(x) \right)}{dx} $ . So, we will let $ f(x)f'(x)=h(x) $ .
Now, we know that if a function is zero, its derivative is also zero. So, if h(x) is zero, h’(x) will also be zero. So, we need to find the number of points where $ f(x)f'(x)=h(x) $ is zero.
First let us draw a graph of f(x) using the points given in the question, i.e., $ A\equiv f(a)=0,B\equiv f(b)=2,C\equiv f(c)=1,D\equiv f(d)=2,E\equiv f(e)=0 $ .

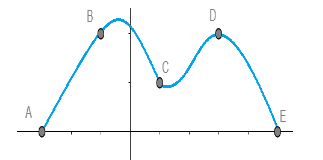
So, as we can see that f(x) is zero at 2 points, A and E, while there are 3 turns in the graph, i.e., one near to B, one after C and one after D. This is just a representative diagram but the turns must be there as the value at E is less than D and the graph is increasing as it reaches D, same with the other turns as well.
So, the number of roots of f(x) are 2 and the number of points where f’(x) is zero is 3. And we know that $ f(x)f'(x)=h(x) $ is zero when one of the two f(x) or f’(x) is zero. So, it will be zero at 5 points for sure.
Now, we know that if a function is zero at n points then its derivative will have at least n-1 zeroes. So, h’(x) will be zero at 4 points at least and h’(x) is equal to $ g(x)={{\left( f'(x) \right)}^{2}}+f''(x)f(x) $ . So, we can conclude that the function g(x), has a minimum of 4 zeroes in the interval [a,e].

Note: Always remember that for using the graph to find the points where the derivative of a function is zero, it must be clear that the function is differentiable and continuous. Also, the key to the above question is identifying h(x), which has no prescribed way to find, but you need to figure it out based on your observation skills.