
If h, k are the perpendicular distances from (1,2,3) to the x-axis, z-axis respectively. Then hk is equal to:
Answer
497.7k+ views
Hint: The distance of a point from an axis is given by the root of the sum of the squares of the coordinates of the points excluding the coordinate corresponding to the axis from which we are finding the distance. For example: the distance of a point P(a,b,c) from the x-axis is given by
Complete step-by-step solution:
Let us start the solution to the above question by drawing a representative diagram of the situation given in the question.
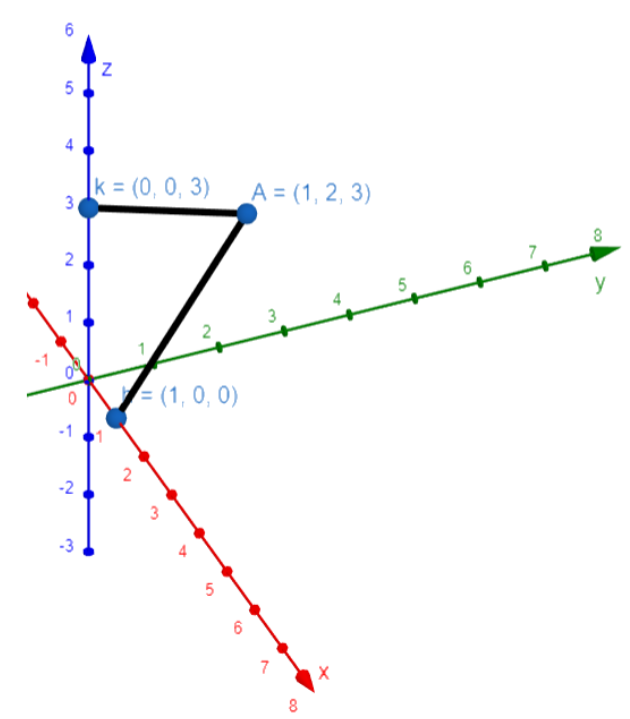
The distance of a point from an axis is given by the root of the sum of the squares of the coordinates of the points excluding the coordinate corresponding to the axis from which we are finding the distance.
So, “h” is the distance from the x-axis, so we will add the squares of y-coordinate and z-coordinate of the point and take the root.
Also, k is the distance from the z-axis, so we will add the squares of y-coordinate and x-coordinate of the point and take the root.
Now, let us find the product of h and k, i.e., hk.
Hence, the answer to the above question is
Note: If you are not aware of the point that the distance of a point from an axis is given by the root of the sum of the squares of the coordinates of the points excluding the coordinate corresponding to the axis from which we are finding the distance, you will have to consider a general point on the axis from which you are finding the distance, which will have two coordinates zero and one variable coordinate. Use the distance formula to get the distance in terms of variable coordinate and minimize it to get the perpendicular distance.
Complete step-by-step solution:
Let us start the solution to the above question by drawing a representative diagram of the situation given in the question.

The distance of a point from an axis is given by the root of the sum of the squares of the coordinates of the points excluding the coordinate corresponding to the axis from which we are finding the distance.
So, “h” is the distance from the x-axis, so we will add the squares of y-coordinate and z-coordinate of the point and take the root.
Also, k is the distance from the z-axis, so we will add the squares of y-coordinate and x-coordinate of the point and take the root.
Now, let us find the product of h and k, i.e., hk.
Hence, the answer to the above question is
Note: If you are not aware of the point that the distance of a point from an axis is given by the root of the sum of the squares of the coordinates of the points excluding the coordinate corresponding to the axis from which we are finding the distance, you will have to consider a general point on the axis from which you are finding the distance, which will have two coordinates zero and one variable coordinate. Use the distance formula to get the distance in terms of variable coordinate and minimize it to get the perpendicular distance.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹42,330 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




