Question

If \[\operatorname{Sin} \theta > 0,\operatorname{Sec} \theta < 0\], then $\theta $ lies in which quadrant
A: First
B: Second
C: Third
D: Fourth

Answer 1

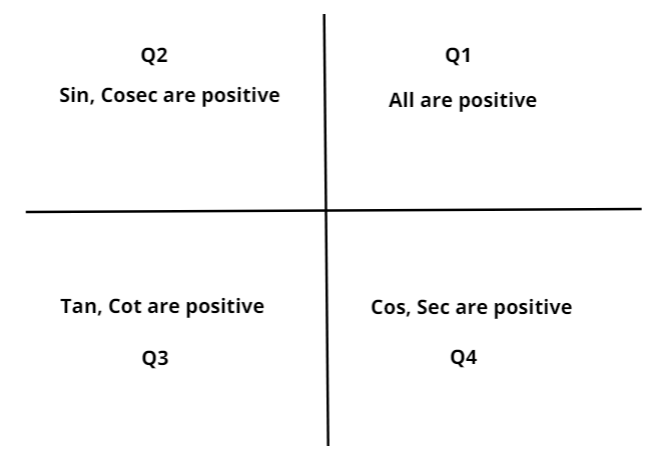
Hint: We know in second quadrant only $\operatorname{Sin} \theta \& \operatorname{Cos} ec\theta $ are positive and rest all $\operatorname{Cos} \theta ,\operatorname{Sec} \theta ,\operatorname{Tan} \theta ,Cot\theta $ are negative So for second quadrant we can write
\[\operatorname{Sin} \theta > 0,\operatorname{Cos} ec\theta > 0,\operatorname{Sec} \theta < 0,\operatorname{Cos} \theta < 0,\operatorname{Tan} \theta < 0,Cot\theta < 0\] hence we can find the answer

Complete step-by-step answer:
As we know that the angles are classified into four quadrants, that is, $1^{st},2^{nd},3^{rd},4^{th}$. So basically a round circle is of a circle is of ${360^ \circ }$ angle so to make a circle we need an angle of ${360^ \circ }$ so this ${360^ \circ }$ is divided into $4$ parts
${\rm I}$ The first part is called $1stQuadrant$ in which the angle lies between ${0^\circ}to{90^\circ}$. If the angle is between ${0^\circ} to {90^\circ}$ then that angle lies in first quadrant and in first quadrant we know \[\operatorname{Sin} \theta ,\operatorname{Cos} ec\theta ,\operatorname{Sec} \theta ,\operatorname{Cos} \theta ,\operatorname{Tan} \theta ,Cot\theta \] all are positive so we can write in the first quadrant \[\operatorname{Sin} \theta > 0,\operatorname{Cos} ec\theta > 0,\operatorname{Sec} \theta > 0,\operatorname{Cos} \theta > 0,\operatorname{Tan} \theta > 0,Cot\theta > 0\]
${\rm I}{\rm I}$ Now if angle lies between ${90^\circ} to {180^\circ}$ then that range is termed as second quadrant for example: If $\theta = {120^\circ}$ then it lies in second quadrant now we know that in second quadrant $\operatorname{Sin} \theta \& \operatorname{Cos} ec\theta $ are positive and rest all $\operatorname{Cos} \theta ,\operatorname{Sec} \theta ,\operatorname{Tan} \theta ,Cot\theta $ are negative so we can say that in second quadrant \[\operatorname{Sin} \theta > 0,\operatorname{Cos} ec\theta > 0,\operatorname{Sec} \theta < 0,\operatorname{Cos} \theta < 0,\operatorname{Tan} \theta < 0,Cot\theta < 0\].
${\rm I}{\rm I}{\rm I}$ If angle lies between ${180^\circ} to {270^\circ}$ then that range is termed as third quadrant. for example: If $\theta = {200^\circ}$ then it lies in third quadrant now we know that in third quadrant $\operatorname{Tan} \theta \& Cot\theta $ are positive and rest all $\operatorname{Cos} \theta ,\operatorname{Sec} \theta ,\operatorname{Sin} \theta ,\operatorname{Cos} ec\theta $ are negative so we can say that in third quadrant \[\operatorname{Sin} \theta < 0,\operatorname{Cos} ec\theta < 0,\operatorname{Sec} \theta < 0,\operatorname{Cos} \theta < 0,\operatorname{Tan} \theta > 0,Cot\theta > 0\].
${\rm I}V$ If angle lies between ${270^\circ} to {360^\circ}$ then that range is termed as fourth quadrant. for example: If $\theta = {300^\circ}$ then it lies in fourth quadrant now we know that in fourth quadrant $\operatorname{Sec} \theta \& Cos\theta $ are positive and rest all $Cot\theta ,\operatorname{Tan} \theta ,\operatorname{Sin} \theta ,\operatorname{Cos} ec\theta $ are negative so we can say that in fourth quadrant \[\operatorname{Sin} \theta < 0,\operatorname{Cos} ec\theta < 0,\operatorname{Sec} \theta > 0,\operatorname{Cos} \theta > 0,\operatorname{Tan} \theta < 0,Cot\theta < 0\].

So here we are given that if $\operatorname{Sin} \theta > 0,\operatorname{Sec} \theta < 0$ so we can conclude that
$({\rm I})$ In $1^{st}$ Quadrant: $\operatorname{Sin} \theta > 0,\operatorname{Sec} \theta > 0$
$({\rm I}{\rm I})$ In $2^{nd}$ Quadrant: $\operatorname{Sin} \theta > 0,\operatorname{Sec} \theta < 0$
$({\rm I}{\rm I}{\rm I})$ In $3^{rd}$ Quadrant: $\operatorname{Sin} \theta < 0,\operatorname{Sec} \theta < 0$
$({\rm I}V)$ In $4^{th}$ Quadrant: $\operatorname{Sin} \theta < 0,\operatorname{Sec} \theta > 0$

Therefore $\operatorname{Sin} \theta > 0,\operatorname{Sec} \theta < 0$ lies in Second quadrant.

Note: We can solve by using graphical method also for example
Graph of $\operatorname{Sin} \theta $

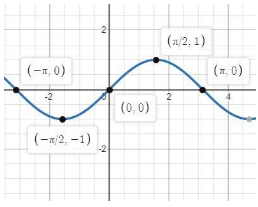
 Graph of $\operatorname{Sec} \theta $

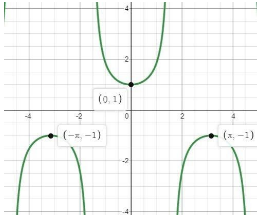
so between $\dfrac{\Pi }{2}to\Pi $ we see $\operatorname{Sin} \theta > 0,\operatorname{Sec} \theta < 0$ and it lies in second quadrant.