Question

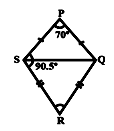
If $PQRS$ is a kite. $\angle P = {70^0},\angle S = {90.5^0},\angle R$ equals .

(A) ${99^0}$
(B) ${91^0}$
(C) ${111^0}$
(D) ${109^0}$

Answer 1

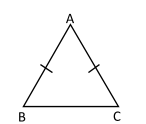
Hint: A triangle in which two sides are equal is called an isosceles triangle.
Angle opposite to the equal sides of an isosceles triangle is equal.
It means if the two sides are equal to a triangle, then their corresponding angles are also equal. Let \[\Delta ABC\], in which side $AB$is equal to side .$AC$
i.e. $AB = AC$
Therefore angle $B$is equal to angle$C$.
i.e. $\angle B = \angle C$

Complete step-by-step answer:
Step 1: Given $PQRS$ is a kite.
Where angle $P$ i.e. $\angle P = {70^0}$ and angle $S$i.e. $\angle S = {90.5^0}$ we will find the value of
$\angle R$

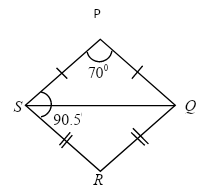
Step 2: firstly consider triangle $PQS$ In $\Delta PQS$, the sides $PS$is equal to $PQ$ i.e. $PS = PQ$
Therefore, the angle $PSQ$ is equal to angle $PQS$ i.e. $\angle PSQ = \angle PQS.$ ----(a)
We know that the sum of the interior angle of a triangle is ${180^0}$.
So angle $P$ plus angle $PSQ$ plus angle $PQS$ is ${180^0}$i.e.
Consider $\angle PSQ = \angle PQS = x$
So from equation $(a)$
${70^0} + x + x = {180^0}$
$\Rightarrow$ $2x = {180^0} - {70^0}$
$\Rightarrow$ $2x = {110^0}$
$\Rightarrow$ $x = \dfrac{{{{110}^0}}}{2} = {55^0}$
Step-3: Give that $\angle S = \angle PSQ + \angle RSQ$
 ${90.5^0} = {55^0} + \angle RSQ$
 ${90.5^0} - {55^0} = \angle RSQ$
${35.5^0} = \angle RSQ$
We have already given angle$S$. So we early found the value of angle $RSQ$ is ${35.5^0}$.
Step – 4: Similarly consider the triangle$RSQ$. In $\Delta RSQ$, the side $SR$is equal to $RQ$ i.e. $SR = RQ$.
Therefore angle $RSQ$ is equal to the angle $RQS$ i.e. $\angle RQS = {35.5^0}$.
We know that the sum of the interior angle of the triangle is ${180^0}$ .
Therefore $\angle RSQ + \angle RQS + \angle R = {180^0}$ --------(b)
Putt the value of $\angle RSQ$and $\angle RQS$is equation (b), we get
$35.5 + 35.5 + \angle R = 180$
$\Rightarrow$ ${71^0} + \angle R = {180^0}$
$\Rightarrow$ $\angle R = 180 - {71^0}$
$\Rightarrow$ $\angle R = {109^0}$
So, we get the value of angle $R$is ${109^0}$ $\angle R = 109$ .
Hence, option (D) is the right Answer.

Note: The sides opposite to equal angles of a triangle are equal.
(SAS congruence) two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.