Question

If $\sin \mathrm{A}=\dfrac{3}{4},$ calculate $\cos \mathrm{A}$ and $\tan \mathrm{A}$.
A.$\cos A=\dfrac{\sqrt{3}}{4}$
$\tan A=\dfrac{2}{5}$
B.$\cos A=\dfrac{\sqrt{7}}{4}$
$\tan A=\dfrac{3}{\sqrt{7}}$
C.$\cos A=\dfrac{\sqrt{3}}{2}$
$\tan A=\dfrac{2}{\sqrt{5}}$
D.$\cos A=\dfrac{\sqrt{5}}{7}$
$\tan A=\dfrac{7}{\sqrt{3}}$

Answer 1

Hint: There are six trigonometric ratios, sine, cosine, tangent, cosecant, secant and cotangent. These six trigonometric ratios are abbreviated as $\sin , \cos ,$ tan, $\mathrm{csc},$ sec, cot. These are referred to as ratios since they can be expressed in terms of the sides of a right-angled triangle for a specific angle $\theta$. Trigonometry is defined as the branch of math that deals with calculations related to the sides and angles of triangles.

Complete step-by-step answer:
The Pythagorean equation relates the sides of a right triangle in a simple way, so that if the
lengths of any two sides are known the length of the third side can be found. Another corollary.

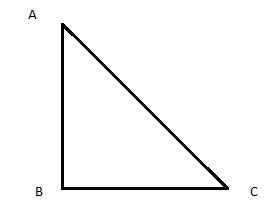
The theorem is that in any right triangle, the hypotenuse is greater than any one of the other sides, but less than their sum.
In a right triangle, the hypotenuse is the longest side, an "opposite" side is the one across from a given angle, and an "adjacent" side is next to a given angle. We use special words to describe the sides of right triangles.
Given, $\sin \mathrm{A}=\dfrac{3}{4}$
$\Rightarrow \dfrac{\mathrm{BC}}{\mathrm{AC}}=\dfrac{3}{4}$
$\Rightarrow \mathrm{BC}=3 \mathrm{k}$ and $\mathrm{AC}=4 \mathrm{k}$
where $\mathrm{k}$ is the constant of proportionality. By Pythagoras theorem, we have $\mathrm{AB}^{2}=\mathrm{AC}^{2}-\mathrm{BC}^{2}=(4 \mathrm{k})^{2}-(3 \mathrm{k})^{2}=7 \mathrm{k}^{2}$
$\Rightarrow \mathrm{AB}=\sqrt{7} \mathrm{k}$
$\mathrm{So}, \cos \mathrm{A}=\dfrac{\mathrm{AB}}{\mathrm{AC}}=\dfrac{\sqrt{7} \mathrm{k}}{4 \mathrm{k}}=\dfrac{\sqrt{7}}{4}$
And $\tan \mathrm{A}=\dfrac{\mathrm{BC}}{\mathrm{AB}}=\dfrac{3 \mathrm{k}}{\sqrt{7} \mathrm{k}}=\dfrac{3}{\sqrt{7}}$
Hence, the correct answer is option B.

Note: The shape of the sine curve is the same for each full rotation of the angle and so the function is called 'periodic'. The period of the function is $360^{\circ}$ or $2 \pi$ radians. We can rotate the point as many times as we like. In mathematical terms we say the 'domain' of the sine function is the set of all real numbers.
The cosine function is a periodic function which is very important in trigonometry. The simplest way to understand the cosine function is to use the unit circle. The $\mathrm{x}$ -coordinate of the point where the other side of the angle intersects the circle is $\cos (\theta),$ and the $y$ -coordinate is $\sin (\theta)$.