Question

If T be any point on the tangent at any point P of a parabola, and if TL be perpendicular to the focal radius SP and TN be perpendicular to the directrix, prove that SL = TN.

Answer 1

Hint: Choosing any point on directrix in form of $\left( -a,0 \right)$, a point on focal point in form of $\left( a,0 \right)$, while a point on parabola as $\left( a{{t}^{2}},2at \right)$ will make the problem very comfortable.

Complete step-by-step answer:
Here, we have a parabola, thus considering a general standard equation for a parabola as, ${{y}^{2}}=4ax$ when the directrix of a parabola is parallel to the y-axis, where $a$ is the distance from the origin to the focus.

Now, considering the given conditions, we have
T, a point on the tangent of a parabola at any point P, and TL be the perpendicular to the focal radius SP and TN be perpendicular to the directrix.

Now, we will have to define what are the major components in a parabola, i.e.,
Focal radius is the line segment stretched from focus of parabola to any point such as P on the parabola, while directrix is the line parallel to the major axis of a parabola, in this case it’s parallel to the y-axis.
Thus, as per question, we have

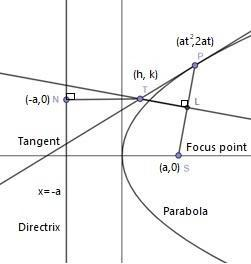
Any general point in a parabola is $P\left( a{{t}^{2}},2at \right)$ and point on a tangent be $T\left( h,k \right)$.
Thus, the equation of tangent $TP$ can be,
$ty=x+a{{t}^{2}}...\text{ }\left( 1 \right)$
Since, this line passes through point $T\left( h,k \right)$, then it must satisfy the equation (1) as well, i.e.,
$\begin{align}
  & \Rightarrow ty=x+a{{t}^{2}} \\
 & \Rightarrow t\left( k \right)=\left( h \right)+a{{t}^{2}} \\
 & \Rightarrow tk=h+a{{t}^{2}}...\text{ }\left( 2 \right) \\
\end{align}$
Now, forming the equation for line $SP$, we need points lying on the line and its slope, and general equation for slope of a line is,
Slope of line $y=mx+c$ is $m$, i.e., $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the points in given line.
Similarly, slope for the line $SP$ with points $S\left( a,0 \right)$ and $P\left( a{{t}^{2}},2at \right)$, we have
Slope of $SP$= ${{m}_{SP}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{2at-0}{a{{t}^{2}}-a}=\dfrac{2at}{a\left( {{t}^{2}}-1 \right)}=\dfrac{2t}{{{t}^{2}}-1}...\text{ (3)}$
Now, as line $TL$ is perpendicular to line $SP$, then its slope can be defined as,
${{m}_{TL}}=\dfrac{-1}{{{m}_{SP}}}$
As per the rules of slope of perpendicular lines.
Thus, from equation (3), we get
${{m}_{TL}}=\dfrac{-1}{\left( \dfrac{2t}{{{t}^{2}}-1} \right)}=\dfrac{-\left( {{t}^{2}}-1 \right)}{2t}=\dfrac{1-{{t}^{2}}}{2t}...\text{ }\left( 4 \right)$
Now, the equation for line $TL$ from a general equation of a line, i.e.,
\[\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)\]
Thus, for line $TL$ equation with point $T\left( h,k \right)$ from equation (4) will be,
 \[\begin{align}
  & \Rightarrow \left( y-{{y}_{1}} \right)={{m}_{TL}}\left( x-{{x}_{1}} \right) \\
 & \Rightarrow y-k=\left( \dfrac{1-{{t}^{2}}}{2t} \right)\left( x-h \right) \\
\end{align}\]
On cross-multiplying both sides, we get
\[\begin{align}
  & \Rightarrow y-k=\left( \dfrac{1-{{t}^{2}}}{2t} \right)\left( x-h \right) \\
 & \Rightarrow 2t\left( y-k \right)=\left( 1-{{t}^{2}} \right)\left( x-h \right) \\
 & \Rightarrow 2ty-2tk=x\left( 1-{{t}^{2}} \right)-h\left( 1-{{t}^{2}} \right) \\
 & \Rightarrow 2ty-x\left( 1-{{t}^{2}} \right)+h\left( 1-{{t}^{2}} \right)-2tk=0 \\
 & \Rightarrow x\left( {{t}^{2}}-1 \right)+2ty+h\left( 1-{{t}^{2}} \right)-2tk=0....\text{ }\left( 5 \right) \\
\end{align}\]
Let us now say distance $SL={{d}_{1}}$, i.e., the perpendicular distance from line $TL$.
Then, from equation of the perpendicular distance of a point $\left( {{x}_{1}},{{y}_{1}} \right)$ from a line, we have
$d=\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$
Thus, for distance of a point $S\left( a,0 \right)$ from line $TL$, we have
$\begin{align}
  & {{d}_{1}}=SL=\left| \dfrac{a\left( {{t}^{2}}-1 \right)+\left( 0 \right)\left( 2y \right)+h\left( 1-{{t}^{2}} \right)-2tk}{\sqrt{{{\left( {{t}^{2}}-1 \right)}^{2}}+{{\left( 2t \right)}^{2}}}} \right| \\
 & =\left| \dfrac{a{{t}^{2}}-a+0+h-h{{t}^{2}}-2tk}{\sqrt{{{\left( {{t}^{2}}-1 \right)}^{2}}+4{{t}^{2}}}} \right| \\
 & =\left| \dfrac{a{{t}^{2}}-a+h-h{{t}^{2}}-2tk}{\sqrt{{{\left( {{t}^{2}}-1 \right)}^{2}}+4{{t}^{2}}}} \right|
\end{align}$
Now, from equation (2), we have $kt=h+a{{t}^{2}}$.
On substituting this value in above equation, we get
$\begin{align}
  & {{d}_{1}}=\left| \dfrac{a{{t}^{2}}-a+h-h{{t}^{2}}-2tk}{\sqrt{{{\left( {{t}^{2}}-1 \right)}^{2}}+4{{t}^{2}}}} \right| \\
 & =\left| \dfrac{a{{t}^{2}}-a+h-h{{t}^{2}}-2\left( h+a{{t}^{2}} \right)}{\sqrt{{{t}^{4}}+1-2{{t}^{2}}+4{{t}^{2}}}} \right| \\
 & =\left| \dfrac{a{{t}^{2}}-a+h-h{{t}^{2}}-2h-2a{{t}^{2}}}{\sqrt{{{t}^{4}}+1+2{{t}^{2}}}} \right| \\
 & =\left| \dfrac{-h-a-a{{t}^{2}}-h{{t}^{2}}}{\sqrt{{{\left( {{t}^{2}}+1 \right)}^{2}}}} \right| \\
 & =\left| \dfrac{-h\left( 1+{{t}^{2}} \right)-a\left( 1+{{t}^{2}} \right)}{{{t}^{2}}+1} \right| \\
 & =\left| \dfrac{-\left( h+a \right)\left( 1+{{t}^{2}} \right)}{{{t}^{2}}+1} \right|
\end{align}$
Cancelling out the common terms from numerator and denominator, we get
$\begin{align}
  & {{d}_{1}}=\left| \dfrac{-\left( h+a \right)\left( 1+{{t}^{2}} \right)}{{{t}^{2}}+1} \right| \\
 & =\left| -\left( h+a \right) \right| \\
 & =h+a
\end{align}$
Thus, $SL={{d}_{1}}=h+a...\text{ }\left( 6 \right)$
Similarly, for length $TN$, i.e., distance of point $T$ to point $N\left( -a,0 \right)$ on the line of directrix, we have
Let’s say, $TN={{d}_{2}}$
$\begin{align}
  & {{d}_{2}}=\left| \dfrac{h\left( 1 \right)+k\left( 0 \right)+a}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \right| \\
 & =\left| \dfrac{h+a}{1} \right| \\
 & =h+a
\end{align}$
Thus, $TN={{d}_{2}}=h+a...\text{ }\left( 7 \right)$
Hence, from equation (6) and (7), we can say that ${{d}_{1}}={{d}_{2}}=SL=TN=h+a$.

Note: An important point to remember can be, while considering general points on parabola or on directrix or on focal point, they should be considered properly as per their properties rather than a general $\left( x,y \right)$ format to avoid confusions while forming equations.