
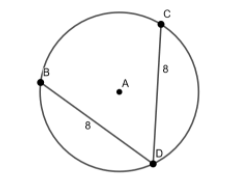
If the angle subtended by the minor arc BD at the centre is
A.
B.
C.
D.

Answer
503.7k+ views
Hint: In the question, it is given that the two chords BD and CD are of 8 units in length and angle
Complete step-by-step answer:
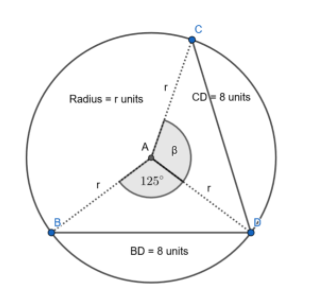
Consider the two triangles
BD = 8 units.
CD = 8 units.
As seen in the above figures, the point A is the centre of the circle. The points B, C, D lie on the circle of radius of r units. So,
Comparing the sides of the two triangles
AD is the common side of the two triangles. So,
From the SSS (Side, Side, Side) property of the congruency of triangles which states that two triangles are congruent if their corresponding sides are equal, we can conclude that the triangles
In the congruent triangles the angles opposite to the corresponding sides are equal.
Option C is the right answer.
Note:The two chords are meeting at the same point D in the given question. But even if there is no common point for the two chords, if the lengths of chords are equal, the angles subtended by the chords at the centre are equal. This is a property which will help in many questions of similar kind.
Complete step-by-step answer:

Consider the two triangles
BD = 8 units.
CD = 8 units.
As seen in the above figures, the point A is the centre of the circle. The points B, C, D lie on the circle of radius of r units. So,
Comparing the sides of the two triangles
AD is the common side of the two triangles. So,
From the SSS (Side, Side, Side) property of the congruency of triangles which states that two triangles are congruent if their corresponding sides are equal, we can conclude that the triangles
In the congruent triangles the angles opposite to the corresponding sides are equal.
Option C is the right answer.
Note:The two chords are meeting at the same point D in the given question. But even if there is no common point for the two chords, if the lengths of chords are equal, the angles subtended by the chords at the centre are equal. This is a property which will help in many questions of similar kind.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

What is the difference between resemblance and sem class 12 social science CBSE




