Question

If the centroid of an equilateral triangle is (1, 1) and it's one vertex is (– 1, 2), then the equation of its circumcircle is:
(a) \[{{x}^{2}}+{{y}^{2}}-2x-2y-3=0\]
(b) \[{{x}^{2}}+{{y}^{2}}+2x-2y-3=0\]
(c) \[{{x}^{2}}+{{y}^{2}}+2x+2y-3=0\]
(d) None of these

Answer 1

Hint: We know that all the centers like centroid, circumcenter, incenter, etc. coincide in the equilateral triangle. So, by considering (1, 1) as a circumcenter, find the radius of the triangle which is the distance between (1, 1) and vertex (– 1, 2). Then use the center radius form of the equation that is \[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}\] to find the equation of the circumcircle.

Complete step-by-step answer:
Here we are given that the centroid of the equilateral triangle is (1, 1) and its vertex is (– 1, 2) then we have to find the equation of the circumcircle of this triangle. Diagrammatically, we can show the situation as

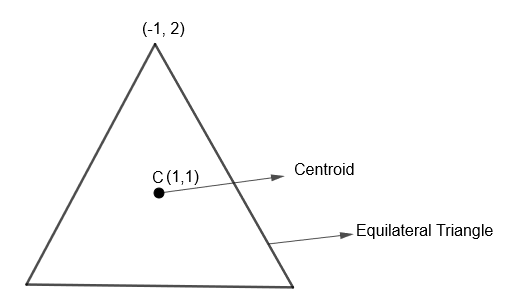
We know that in an equilateral triangle, all centers like centroid, circumcenter, incenter, orthocenter, etc. coincide. Therefore, we get the circumcenter of the given triangle as (1, 1). Also, we know that the circumcircle of a triangle is the circle that circumscribes it or passes through its vertices. So, we get,

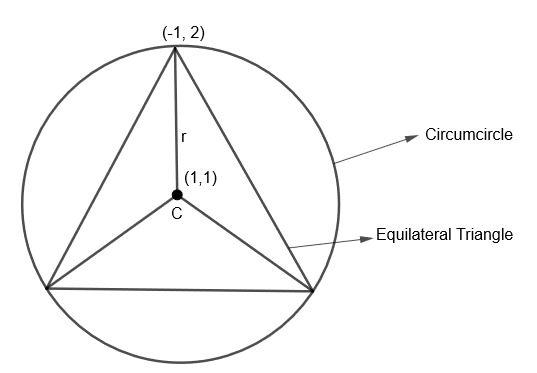
Here, we have drawn the circumcircle of the equilateral triangle which has a center at C (1, 1). Now, we know that the radius of the circumcircle is the distance between the center and the vertex of the triangle.
So, we get the radius of the given circumcircle (r) = Distance between the center (1, 1) and vertex (– 1, 2).
By using distance formula between the points (1, 1) and (– 1, 2). We can calculate the distance between them. According to the distance formula, the distance between any two points say \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is:
\[D=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
By taking \[({{x}_{1}},{{y}_{1}})\] as (1, 1) and \[({{x}_{2}},{{y}_{2}})\] as (– 1, 2), we get the distance between (1, 1) and (– 1, 2)
\[\begin{align}
  & =\sqrt{{{\left( -1-1 \right)}^{2}}+{{\left( 2-1 \right)}^{2}}} \\
 & r=\sqrt{{{\left( -2 \right)}^{2}}+{{\left( 1 \right)}^{2}}} \\
 & r=\sqrt{4+1}=\sqrt{5} \\
\end{align}\]
So, we get the radius of the circle as \[\sqrt{5}\] units.
Now, we know that the equation of the circle having center \[({{x}_{1}},{{y}_{1}})\] and radius r is given be
\[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}\]
So, by using this, we get the equation of our circumcircle which has center (1, 1) and radius \[=\sqrt{5}\] units as
\[{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}\]
We know that \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\]. By using this in the above equation, we get,
\[{{x}^{2}}+1-2x+{{y}^{2}}+1-2y=5\]
By rearranging the equation, we get,
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2x-2y+1+1-5=0\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2x-2y-3=0\]
Here, we get the equation of the circumcircle as \[{{x}^{2}}+{{y}^{2}}-2x-2y-3=0\].
Hence, option (a) is the right answer.

Note: Here, students must remember that the equilateral triangle is the most symmetrical of all triangles and all the centers such as in the center, orthocenter, centroid, circumcenter, etc. are the same in it. Also, the circumcircle of any polygon is the circle which passes through all the vertices of that polygon. Students should take special care of the signs while applying the distance formula between two points.