Question

If the diagonal and the area of a rectangle are 25 m and \[168{{m}^{2}}\], what is the length of the rectangle?
(a) 17 m
(b) 31 m
(c) 12 m
(d) 24 m

Answer 1

Hint:First of all, draw a rectangle ABCD and take AD = b, DC = l and AC = d = 25m. Now, use \[l\times b=168{{m}^{2}}\] and from this, get the value of l in terms of b. Now, use Pythagoras Theorem in triangle ADC and substitute all the values in terms of b and get the value of b and from this get the value of l.

Complete step-by-step answer:
In this question, we have to find the length of the rectangle if the diagonal and the area of the rectangle are 25m and \[168{{m}^{2}}\] respectively. Now, let us consider our question.

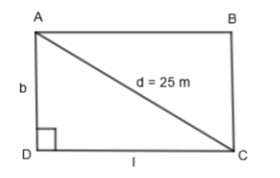
Let us assume a rectangle ABCD with AD = BC = b and AB = DC = l. Also, AC = BD = d. We are given that the area of the rectangle is \[168{{m}^{2}}\]. So, we get,
\[l\times b=168{{m}^{2}}\]
\[l=\dfrac{168}{b}....\left( i \right)\]
Now, let us apply Pythagoras Theorem in triangle ADC right-angled at D. So, we get,
\[A{{D}^{2}}+D{{C}^{2}}=A{{C}^{2}}\]
We know that AD = b, DC = l and AC = 25 m. By using these, we get,
\[{{b}^{2}}+{{l}^{2}}={{\left( 25 \right)}^{2}}\]
By substituting \[l=\dfrac{168}{b}\] from equation (i), we get,
\[{{b}^{2}}+{{\left( \dfrac{168}{b} \right)}^{2}}={{\left( 25 \right)}^{2}}\]
\[{{b}^{2}}+{{\dfrac{168}{{{b}^{2}}}}^{2}}={{\left( 25 \right)}^{2}}\]
\[{{\dfrac{{{b}^{4}}+168}{{{b}^{2}}}}^{2}}={{\left( 25 \right)}^{2}}\]
\[{{b}^{4}}+{{168}^{2}}={{\left( 25 \right)}^{2}}{{b}^{2}}\]
\[{{b}^{4}}-{{\left( 25 \right)}^{2}}{{b}^{2}}+{{\left( 168 \right)}^{2}}=0\]
\[{{b}^{4}}-625{{b}^{2}}+28224=0\]
Let us take \[{{b}^{2}}=x\], so we get,
\[{{x}^{2}}-625x+28224=0\]
Above is a quadratic equation of the form \[a{{x}^{2}}+bx+c=0\] and for the quadratic equation, we know that
\[x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\]
So, we get,
\[x=\dfrac{-\left( -625 \right)\pm \sqrt{{{\left( -625 \right)}^{2}}-4\left( 1 \right)\left( 28224 \right)}}{2}\]
\[x=\dfrac{625\pm \sqrt{390625-112896}}{2}\]
\[x=\dfrac{625\pm \sqrt{277729}}{2}\]
\[x=\dfrac{625\pm 527}{2}\]
So, we get,
\[x=\dfrac{98}{2}\text{ or }x=\dfrac{1152}{2}\]
x = 49 or x = 576
By replacing x with \[{{b}^{2}}\], we get,
\[{{b}^{2}}=49\text{ or }{{b}^{2}}=576\]
\[b=\sqrt{49}\text{ or }b=\sqrt{576}\]
So, we get,
b = 7 m or b = 24 m.
By substituting the value of b = 7 in equation (i), we get,
\[l=\dfrac{168}{7}\]
l = 24 m.
So, by substituting the value of b = 24 m in equation (i), we get,
\[l=\dfrac{168}{24}\]
l = 7 m.
We know that the length is generally greater than the breadth, so we get length as 24 m and breadth as 7 m.
Hence, option (d) is the right answer.

Note: In this question, students can take any diagonal and corresponding right triangle as the diagonals of the rectangle are equal to the length. Also, in the above question, to save from the large calculations, students can subtract 2lb from both sides of the equation \[{{l}^{2}}+{{b}^{2}}={{\left( 25 \right)}^{2}}\] and make the equation \[{{\left( l-b \right)}^{2}}={{\left( 25 \right)}^{2}}-2lb\] and substitute the value of lb as 168. From this, we will only get the quadratic equation unlike the quadratic equation, we get in the above solution. Though both the ways are correct and students should use them according to convenience.