Question

If the first point of trisection of AB is (t, 2t) and the ends A, B move on ‘x’ and ‘y’ axis respectfully, then the focus of midpoint of AB is
A.x = y
B.2x = y
C.4x = y
D.x = 4y

Answer 1

Hint: We know the section formula, the coordinates of the point P(x, y) which divides the line segment joining the points \[A({x_1},{y_1})\] and \[B({x_2},{y_2})\] internally, in the ratio \[{m_1}:{m_2}\] are \[\left( {\dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},\dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}} \right)\] . We choose the midpoint as \[M(h,k)\] and using the above formula we find the coordinate values ‘h’ and ‘k’ to obtain the required result.

Complete step-by-step answer:
Let \[M(h,k)\] be the midpoint of line AB. Given A, B move on the ‘x’ and ‘y’ axis respectively. Then it is obvious that the coordinates of A and B are \[A(2h,0)\] and \[B(0,2k)\] .
Since point \[P(t,2t)\] is first trisection it divides A and B into \[1:2\] ratio. See in the below diagram for understanding point of view.

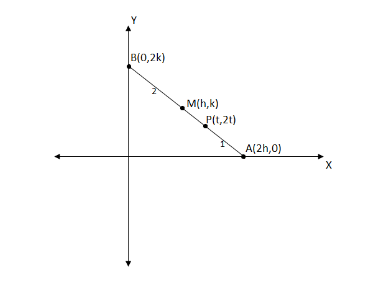
We have \[A({x_1},{y_1}) = A(2h,0)\] , \[B({x_2},{y_2}) = B(0,2k)\] and which divides in the ratio \[1:2\] . Using the section formula we find the coordinates of the point P.
Using the formula \[\left( {\dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},\dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}} \right)\]
 \[ \Rightarrow = P\left( {\dfrac{{\left( {1 \times 0} \right) + \left( {2 \times 2h} \right)}}{{1 + 2}},\dfrac{{\left( {1 \times 2k} \right) + \left( {2 \times 0} \right)}}{{1 + 2}}} \right)\]
 \[ \Rightarrow = P\left( {\dfrac{{0 + 4h}}{3},\dfrac{{2k + 0}}{3}} \right)\]
 \[ \Rightarrow = P\left( {\dfrac{{4h}}{3},\dfrac{{2k}}{3}} \right)\]
But we already have point p coordinates as \[P(t,2t)\] .
Comparing ‘x’ and ‘y’ coordinates in both Points P we have
The ‘x’ coordinate \[\dfrac{{4h}}{3} = t\]
Multiply by 3 on both sides.
 \[ \Rightarrow 4h = 3t{\text{ - - - - - - - (1)}}\]
The ‘y’ coordinate \[\dfrac{{2k}}{3} = 2t\]
Cancelling 2 on both sides,
 \[ \Rightarrow \dfrac{k}{3} = t\]
Multiply by 3 on both sides,
 \[ \Rightarrow k = 3t{\text{ - - - - - - - (2)}}\]
Now substituting equation (2) in equation (1) we have \[ \Rightarrow 4h = k\] .
But we have options in ‘x’ and ‘y’ variables, so we have
 \[ \Rightarrow 4x = y\] (Because \[(h,y) = (x,y)\] )
So, the correct answer is “Option C”.

Note: In general Trisection is the division of a quantity or figure into three equal parts. In the above problem when P is the first trisection there is another two trisection. Hence we take the ratio as \[1:2\] . Remember the formula of section formula. Careful in the substitution and calculation part.