Question

If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is
a. 4
b. 2
c. 1
d. 3

Answer 1

Hint: We will first find the HCF of the numbers 65 and 117, by writing their factors, and taking the factor with the highest value which is common to both the numbers. And, then we will equate this value to the expression, 65m – 117 and get the value of m from it.

Complete step-by-step answer:
We have been given in the question that if the HCF of 65 and 117 is expressible in the form 65m – 117, then we have to find the value of m.
Before we proceed with the question, let us first understand what an HCF or the highest common factor is. HCF is the factor with the highest value that is common to the numbers whose HCF is taken.
For example, the HCF of the numbers 40 and 15 is 5.
So, we will find the HCF of the numbers 65 and 117. So, we can write their factors first, so we get,
$\begin{align}
  & 65=5\times 13 \\
 & 117=3\times 3\times 13 \\
\end{align}$
So, from the factors of 65 and 117, we can see that 13 is the highest common factor. Hence, we get the HCF as 13.
Now, we also have the expression for the HCF of 65 and 117 as 65m – 117. So, we will equate this expression to the value of HCF. So, we will get,
65m – 117 = 13
On adding 117 to both the sides of the above equation, we get,
65m = 13 + 117
65m = 130
On dividing both the sides by 65, we get,
$m=\dfrac{130}{65}$
m = 2
Therefore, we get the value of m as 2.

So, the correct answer is “Option b”.

Note: Most of the students get confused between LCM and HCF. They may write the HCF of 65 and 117 as $5\times 3\times 13$, but this is actually the LCM of those numbers. One can also find the HCF using the long division method, which is as shown below.

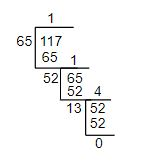
So, from here also we get the HCF as 13.