Question

If the lengths of the diagonals of a rhombus are \[a + b\] and \[a - b\], what is the area of the rhombus?

Answer 1

Hint: A four sided figure that has all four sides of equal length but possess diagonals of unequal lengths is said to be a rhombus. In a space that is two-dimensional, the amount of space taken by the rhombus or amount of space a rhombus encloses is denoted as its area.

Complete step-by-step answer:
The details we are given in the question are that the quadrilateral whose area we need to find is a rhombus. Every rhombus consists of four sides that have equal lengths.
Also we know that in a rhombus, the two diagonals will have two different lengths. Here the lengths of each diagonal is said to be \[a + b\] and \[a - b\].

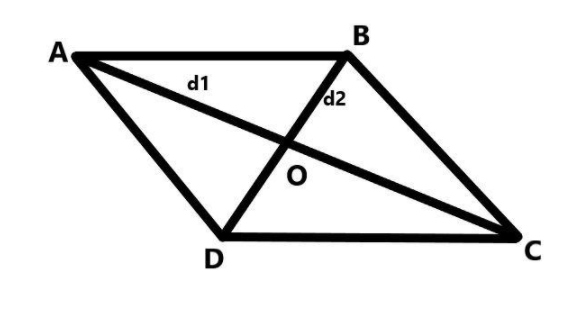
In the given figure, each side is equal so let us denote it as:
 $ \Rightarrow AB = BC = CD = DA $
And each diagonal is given to be $ d_1 $ and $ d_2 $ whose values will be;
 $ \Rightarrow d_1 = a + b $ and $ \Rightarrow d_2 = a - b $
Consider that the center of this rhombus, where both of the diagonals intersect is said to be $ O $ .
Then we know that the diagonals intersect each other at right angles or $ {90^ \circ } $ .
Since every side of the rhombus is equal $ \Rightarrow AB = BC = CD = DA $
The area of the rhombus can also be expressed as $ 4 $ times the area of one small triangle, say $ AOD $ .
 $ \Rightarrow $ Area of rhombus ( $ A $ ) $ = 4 \times $ area of $ \Delta AOD $
 $ \Rightarrow $ Area of rhombus ( $ A $ ) $ = 4 \times (\dfrac{1}{2} \times OD \times (\dfrac{{OA}}{2}))\;sq.\;units $
 $ \Rightarrow $ Area of rhombus ( $ A $ ) $ = 4 \times (\dfrac{1}{2} \times \dfrac{{d_2}}{2} \times (\dfrac{{d_1}}{2}))\;sq.\;units $
 $ \Rightarrow $ Area of rhombus ( $ A $ ) $ = 4 \times (\dfrac{{d_1 \times d_2}}{8})\;sq.\;units $
 $ \Rightarrow $ Area of rhombus ( $ A $ ) $ = \dfrac{{d_1 \times d_2}}{2}\;sq.\;units $
So half of the product of diagonals gives the area of any rhombus.
Now we are given the diagonals of the rhombus to be
 $ d_1 = a + b $ and $ d_2 = a - b $
So substituting the values of the diagonals into the formula or area of rhombus ( $ A $ ):
 $ \Rightarrow $ Area of rhombus ( $ A $ ) $ = \dfrac{{(a + b) \times (a - b)}}{2}\;sq.\;units $
Simplifying we get the area of the given rhombus to be:
 $ \therefore $ Area of rhombus ( $ A $ ) $ = \dfrac{{({a^2} - {b^2})}}{2}\;sq.\;units $
So, the correct answer is “ ( $ A $ ) $ = \dfrac{{({a^2} - {b^2})}}{2}\;sq.\;units $ ”.

Note: A rhombus is similar to a square because all of its sides are equal but it is different from a square because the diagonals of a rhombus vary, but in a square all the diagonals are equal. Square and rhombus also differ in the fact that the diagonals of the rhombus intersect at right angles but diagonals of a square never intersect at right angles.