
If the locus of the moving point X which is always equidistant from M and N, then the locus will be a straight line perpendicular to the NM and passing through the mid-point of NM. If true enter 1 else 0.

Answer
475.8k+ views
Hint: We start solving the problem by assuming the points M and N. We then find the midpoint of these two points and assume the point present in the locus. We use the equidistant condition that is given in the problem and make the necessary calculations to get the required locus. We then compare the locus with the general equation of the straight line and then substitute the midpoint we found to verify whether it is present on the locus or not.
Complete step-by-step solution:
According to the problem, we need to find the locus of the moving point that is equidistant from the points M and N. We also need to check whether the locus is a straight line passing through the midpoint of the line segment connecting the points M and N.
Let us redraw the figure.
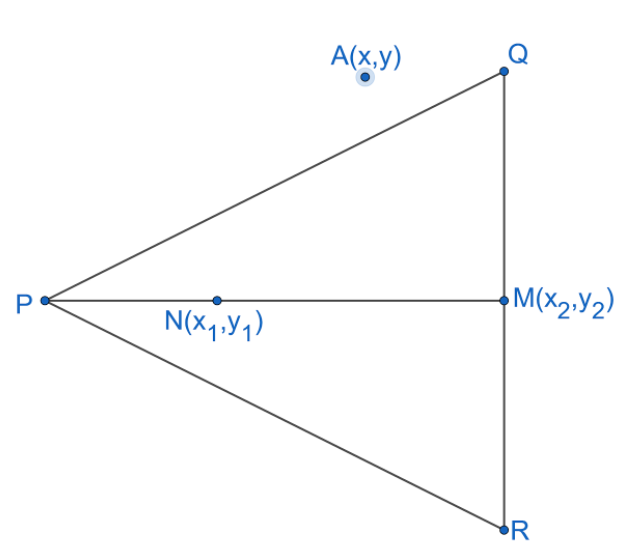
Let us assume the given points be $M\left( {{x}_{2}},{{y}_{2}} \right)$ and $N\left( {{x}_{1}},{{y}_{1}} \right)$. Now, let us find the midpoint of the line segment connecting the points M and N. Let the midpoint be ‘O’.
So, we get $O=\left( \dfrac{{{x}_{2}}+{{x}_{1}}}{2},\dfrac{{{y}_{2}}+{{y}_{1}}}{2} \right)$ -------(1).
Let us assume the point $A\left( x,y \right)$ lies on the required focus.
According to the problem, point A is equidistant from the points M and N.
So, we have $AM=AN$.
We know that the distance between two points $\left( a,b \right)$ and \[\left( c,d \right)\] is $\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}$. We use this in finding the distances of AM and AN.
$\Rightarrow \sqrt{{{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}}}=\sqrt{{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}}$.
Let us square on both sides.
$\Rightarrow {{\left( \sqrt{{{x}^{2}}+x_{2}^{2}-2x{{x}_{2}}+{{y}^{2}}+y_{2}^{2}-2y{{y}_{2}}} \right)}^{2}}={{\left( \sqrt{{{x}^{2}}+x_{1}^{2}-2x{{x}_{1}}+{{y}^{2}}+y_{1}^{2}-2y{{y}_{1}}} \right)}^{2}}$.
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2x{{x}_{2}}-2y{{y}_{2}}+x_{2}^{2}+y_{2}^{2}={{x}^{2}}+{{y}^{2}}-2x{{x}_{1}}-2y{{y}_{1}}+x_{1}^{2}+y_{1}^{2}\].
\[\Rightarrow -2x{{x}_{2}}-2y{{y}_{2}}+2x{{x}_{1}}+2y{{y}_{1}}={{x}^{2}}+{{y}^{2}}-{{x}^{2}}-{{y}^{2}}+x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2}\].
\[\Rightarrow 2x\left( {{x}_{1}}-{{x}_{2}} \right)+2y\left( {{y}_{1}}-{{y}_{2}} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)\] ---(2).
So, we have found the locus of the point equidistant from the points M and N is \[2x\left( {{x}_{1}}-{{x}_{2}} \right)+2y\left( {{y}_{1}}-{{y}_{2}} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)\].
We can see that locus resembles the general equation of straight line $ax+by=c$. So, the locus is a straight line.
Let us substitute mid-point which we got from equation (1) in this locus.
$\Rightarrow 2\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2} \right)\left( {{x}_{1}}-{{x}_{2}} \right)+2\left( \dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\left( {{y}_{1}}-{{y}_{2}} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)$.
$\Rightarrow \left( {{x}_{1}}+{{x}_{2}} \right)\left( {{x}_{1}}-{{x}_{2}} \right)+\left( {{y}_{1}}+{{y}_{2}} \right)\left( {{y}_{1}}-{{y}_{2}} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)$.
$\Rightarrow \left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)$.
We can see that L.H.S=R.H.S. This tells us that the mid-point of the line segment connecting points M and N satisfies the locus which is a straight line.
So, the given statement is true. We need to enter 1.
Note: We should make calculation mistakes while solving this problem. We can also take point A as $\left( h,k \right)$ to avoid the confusion while solving for the locus. We can also find the slope of this line if the coordinates of the points are actually given in the problem. We should know that mid-point is the point that is equidistant from two points. We can also verify it by finding the equation of the straight line passing through the point A and the mid-point of the line segment joining M and N. Similarly, we can expect problems to find the locus of the points whose distance points M and N are at a ratio of $a:b$.
Complete step-by-step solution:
According to the problem, we need to find the locus of the moving point that is equidistant from the points M and N. We also need to check whether the locus is a straight line passing through the midpoint of the line segment connecting the points M and N.
Let us redraw the figure.

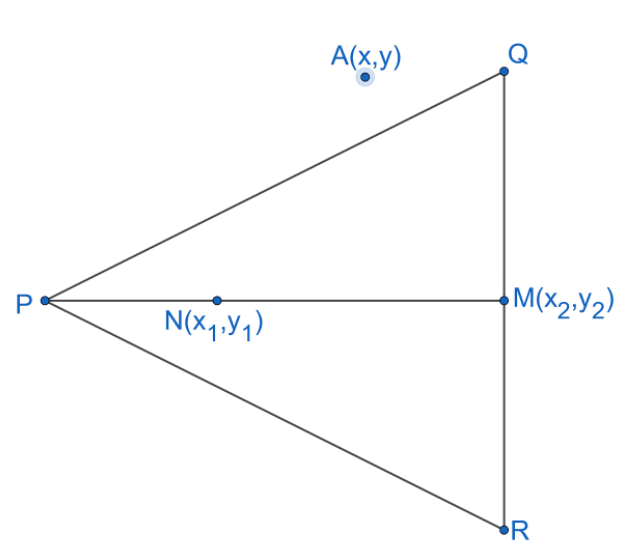
Let us assume the given points be $M\left( {{x}_{2}},{{y}_{2}} \right)$ and $N\left( {{x}_{1}},{{y}_{1}} \right)$. Now, let us find the midpoint of the line segment connecting the points M and N. Let the midpoint be ‘O’.
So, we get $O=\left( \dfrac{{{x}_{2}}+{{x}_{1}}}{2},\dfrac{{{y}_{2}}+{{y}_{1}}}{2} \right)$ -------(1).
Let us assume the point $A\left( x,y \right)$ lies on the required focus.
According to the problem, point A is equidistant from the points M and N.
So, we have $AM=AN$.
We know that the distance between two points $\left( a,b \right)$ and \[\left( c,d \right)\] is $\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}$. We use this in finding the distances of AM and AN.
$\Rightarrow \sqrt{{{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}}}=\sqrt{{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}}$.
Let us square on both sides.
$\Rightarrow {{\left( \sqrt{{{x}^{2}}+x_{2}^{2}-2x{{x}_{2}}+{{y}^{2}}+y_{2}^{2}-2y{{y}_{2}}} \right)}^{2}}={{\left( \sqrt{{{x}^{2}}+x_{1}^{2}-2x{{x}_{1}}+{{y}^{2}}+y_{1}^{2}-2y{{y}_{1}}} \right)}^{2}}$.
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2x{{x}_{2}}-2y{{y}_{2}}+x_{2}^{2}+y_{2}^{2}={{x}^{2}}+{{y}^{2}}-2x{{x}_{1}}-2y{{y}_{1}}+x_{1}^{2}+y_{1}^{2}\].
\[\Rightarrow -2x{{x}_{2}}-2y{{y}_{2}}+2x{{x}_{1}}+2y{{y}_{1}}={{x}^{2}}+{{y}^{2}}-{{x}^{2}}-{{y}^{2}}+x_{1}^{2}+y_{1}^{2}-x_{2}^{2}-y_{2}^{2}\].
\[\Rightarrow 2x\left( {{x}_{1}}-{{x}_{2}} \right)+2y\left( {{y}_{1}}-{{y}_{2}} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)\] ---(2).
So, we have found the locus of the point equidistant from the points M and N is \[2x\left( {{x}_{1}}-{{x}_{2}} \right)+2y\left( {{y}_{1}}-{{y}_{2}} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)\].
We can see that locus resembles the general equation of straight line $ax+by=c$. So, the locus is a straight line.
Let us substitute mid-point which we got from equation (1) in this locus.
$\Rightarrow 2\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2} \right)\left( {{x}_{1}}-{{x}_{2}} \right)+2\left( \dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\left( {{y}_{1}}-{{y}_{2}} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)$.
$\Rightarrow \left( {{x}_{1}}+{{x}_{2}} \right)\left( {{x}_{1}}-{{x}_{2}} \right)+\left( {{y}_{1}}+{{y}_{2}} \right)\left( {{y}_{1}}-{{y}_{2}} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)$.
$\Rightarrow \left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)=\left( x_{1}^{2}-x_{2}^{2} \right)+\left( y_{1}^{2}-y_{2}^{2} \right)$.
We can see that L.H.S=R.H.S. This tells us that the mid-point of the line segment connecting points M and N satisfies the locus which is a straight line.
So, the given statement is true. We need to enter 1.
Note: We should make calculation mistakes while solving this problem. We can also take point A as $\left( h,k \right)$ to avoid the confusion while solving for the locus. We can also find the slope of this line if the coordinates of the points are actually given in the problem. We should know that mid-point is the point that is equidistant from two points. We can also verify it by finding the equation of the straight line passing through the point A and the mid-point of the line segment joining M and N. Similarly, we can expect problems to find the locus of the points whose distance points M and N are at a ratio of $a:b$.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Glucose when reduced with HI and red Phosphorus gives class 11 chemistry CBSE

The highest possible oxidation states of Uranium and class 11 chemistry CBSE

Find the value of x if the mode of the following data class 11 maths CBSE

Which of the following can be used in the Friedel Crafts class 11 chemistry CBSE

A sphere of mass 40 kg is attracted by a second sphere class 11 physics CBSE

Trending doubts
10 examples of friction in our daily life

Difference Between Prokaryotic Cells and Eukaryotic Cells

State and prove Bernoullis theorem class 11 physics CBSE

What organs are located on the left side of your body class 11 biology CBSE

Define least count of vernier callipers How do you class 11 physics CBSE

The combining capacity of an element is known as i class 11 chemistry CBSE




