
If the radius of
A. coordination number of
B.coordination number of
C.length of the unit cell is 552 pm
D.length of the unit cell is 380 pm
Answer
509.7k+ views
Hint: Radius ratio is used to find out the coordination number of the ionic solids.
NaCl is an ionic solid with fcc (face-centred cubic) lattice. So, the edge length of the unit cell can be determined from the arrangement of the ions in the fcc lattice.
Complete step by step answer:
The radius ratio of the ionic solid is the ratio of the radius of the cation to the radius of the anion.
Formula of the radius ratio:
Radius ratio =
In an ionic solid, a cation is surrounded by the highest number of anions around it. Greater radius ratio indicates higher coordination number.
Here, the radius of the cation (
So, radius ratio =
When the radius ratio lies between 0.414 and 0.732, the coordination number of the ions is 6.
So, the coordination number of
fcc structure means there will be eight atoms at the eight corners of the cube and one atom at the centre on each of the six faces of the cube. The structure of the lattice is a as follows:
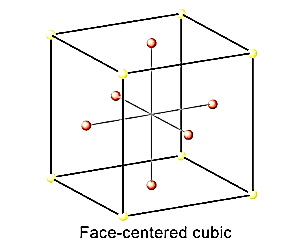
The radius of
length of the unit cell = 2
= 2
= 2
So, the correct options are A and C.
Note: When the radius ratio lies between 0.225 and 0.414, the coordination number of the ions is 4. When the radius ratio lies between 0.414 and 0.732, the coordination number of the ions is 6.
NaCl is an ionic solid with fcc (face-centred cubic) lattice. So, the edge length of the unit cell can be determined from the arrangement of the ions in the fcc lattice.
Complete step by step answer:
The radius ratio of the ionic solid is the ratio of the radius of the cation to the radius of the anion.
Formula of the radius ratio:
Radius ratio =
In an ionic solid, a cation is surrounded by the highest number of anions around it. Greater radius ratio indicates higher coordination number.
Here, the radius of the cation (
So, radius ratio =
When the radius ratio lies between 0.414 and 0.732, the coordination number of the ions is 6.
So, the coordination number of
fcc structure means there will be eight atoms at the eight corners of the cube and one atom at the centre on each of the six faces of the cube. The structure of the lattice is a as follows:

The radius of
length of the unit cell = 2
= 2
= 2
So, the correct options are A and C.
Note: When the radius ratio lies between 0.225 and 0.414, the coordination number of the ions is 4. When the radius ratio lies between 0.414 and 0.732, the coordination number of the ions is 6.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




