Question

If the radius of the circumcircle of an isosceles triangle PQR is equal to PQ \[\left( =PR \right)\], then the angle P is
(A) \[\dfrac{\pi }{6}\]
(B) \[\dfrac{\pi }{3}\]
(C) \[\dfrac{\pi }{2}\]
(D) \[\dfrac{2\pi }{3}\]

Answer 1

Hint: Assume a \[\Delta PQR\] and O is the center of the circumcircle of \[\Delta PQR\] . The isosceles triangle \[PQR\] in which the side \[PQ\] is equal to PR, and the radius of the circumcircle of \[\Delta PQR\] is equal to \[PQ\] . So, \[PQ=PR\] and Radius of circumcircle = PQ =PR. Draw OA and OB perpendicular to the side PQ and PR respectively. We know the property that the perpendicular drawn from the center of a circle to a chord bisects the chord. Use this property and calculate OA and OB in terms of PQ and PR respectively. We know that \[\cos \theta =\dfrac{Base}{Hypotenuse}\] . Now, apply cosine ratio in \[\Delta OAP\] and \[\Delta OBP\]for \[\angle APO\] and \[\angle BPO\] respectively. Use \[\cos \dfrac{\pi }{3}=\dfrac{1}{2}\Rightarrow \dfrac{\pi }{3}={{\cos }^{-1}}\left( \dfrac{1}{2} \right)\] and solve it further to get \[\angle P\] .

Complete step-by-step solution
According to the question, we are given an isosceles triangle \[PQR\] in which the side \[PQ\] is equal to PR, and the radius of the circumcircle of \[\Delta PQR\] is equal to \[PQ\]. So,
\[PQ=PR\] ………………………………….(1)
The radius of the circumcircle of \[\Delta PQR\] = \[PQ\] ……………………………………..(2)
Now, our diagram of the isosceles triangle \[\Delta PQR\] along with its circumcircle is as below,

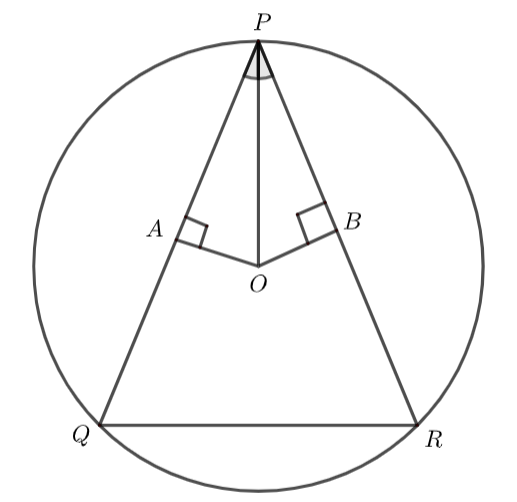
Drawing perpendicular OA and OB to the side PQ and PR respectively.
We know the property that the perpendicular drawn from the center of a circle to a chord bisects the chord ………………………………………..(3)
Since OA and OB is perpendicular to the side PQ and PR respectively so, using the property shown in equation (3), we can say that OA and OB bisect the side PQ and PR respectively, i.e,
\[PA=AQ\] ………………………………………..(4)
\[PB=BQ\] ………………………………………(5)
From the figure, we can say that
\[PQ=PA+AQ\] ……………………………………….(6)
 \[PR=PB+BR\] ……………………………………….(7)
Now, from equation (4) and equation (6), we get
\[\begin{align}
  & \Rightarrow PQ=PA+PA \\
 & \Rightarrow PQ=2PA \\
\end{align}\]
\[\Rightarrow \dfrac{PQ}{2}=PA\] …………………………………….(8)
Similarly, from equation (5) and equation (7), we get
\[\begin{align}
  & \Rightarrow PR=PB+PB \\
 & \Rightarrow PR=2PB \\
\end{align}\]
\[\Rightarrow \dfrac{PR}{2}=PB\] …………………………………….(9)
Now, from equation (1) and equation (9), we get
\[\Rightarrow \dfrac{PQ}{2}=PB\] ………………………………………(10)
In the \[\Delta OAP\]for \[\angle APO\] , we have
Base = PA ……………………………………..(11)
Hypotenuse = OP = Radius ………………………………………(12)
From equation (2) and equation (12), we get
Hypotenuse = \[OP=PQ\] ……………………………….(13)
We know the formula for cosine ratio for a triangle, \[\cos \theta =\dfrac{Base}{Hypotenuse}\] ……………………………………….(14)
Now, from equation (11), equation (13), and equation (14), we get
\[\Rightarrow \cos \angle APO=\dfrac{PA}{PQ}\] ……………………………………………….(15)
From equation (8) and equation (15), we get
\[\begin{align}
  & \Rightarrow \cos \angle APO=\dfrac{\dfrac{PQ}{2}}{PQ} \\
 & \Rightarrow \cos \angle APO=\dfrac{1}{2} \\
\end{align}\]
\[\Rightarrow \angle APO={{\cos }^{-1}}\left( \dfrac{1}{2} \right)\] ………………………………………….(16)
Similarly, in the \[\Delta OBP\]for \[\angle BPO\] , we have
Base = PB ……………………………………..(17)
Hypotenuse = \[OP=PQ\] (from equation (13)) ……………………………….(18)
Now, from equation (14), equation (17), and equation (18), we get
\[\Rightarrow \cos \angle BPO=\dfrac{PB}{PQ}\] ……………………………………………….(19)
From equation (10) and equation (19), we get
\[\begin{align}
  & \Rightarrow \cos \angle BPO=\dfrac{\dfrac{PQ}{2}}{PQ} \\
 & \Rightarrow \cos \angle BPO=\dfrac{1}{2} \\
\end{align}\]
\[\Rightarrow \angle BPO={{\cos }^{-1}}\left( \dfrac{1}{2} \right)\] ………………………………………….(20)
From the diagram, we can see that, \[\angle P=\angle APO+\angle BPO\] ……………………………………….(21)
Now, from equation (16), equation (20), and equation (21), we get
\[\Rightarrow \angle P={{\cos }^{-1}}\left( \dfrac{1}{2} \right)+{{\cos }^{-1}}\left( \dfrac{1}{2} \right)\] …………………………………………(22)
We know that \[\cos \dfrac{\pi }{3}=\dfrac{1}{2}\Rightarrow \dfrac{\pi }{3}={{\cos }^{-1}}\left( \dfrac{1}{2} \right)\] ……………………………………………(23)
Now, from equation (22) and equation (23), we get
\[\Rightarrow \angle P=\dfrac{\pi }{3}+\dfrac{\pi }{3}\]
\[\Rightarrow \angle P=\dfrac{2\pi }{3}\] …………………………………………………..(24)
Therefore, the measure of \[\angle P\] is \[\dfrac{2\pi }{3}\] .
Hence, the correct option is (D).

Note: In this question, since it is given that the sides PQ and PR are equal so, one might think that they may be the radius of the circle. This is wrong because on taking this consideration the circle will no longer circumcircle to the triangle.