Question

If the sides AB, BC, CD and DA of a trapezium ABCD measure 10 cm, 20 cm, 18 cm and 16 cm respectively then find the length of the longer diagonal given that AB is parallel to CD
A) \[\sqrt{760}cm\]
B) \[\sqrt{231}cm\]
C) \[\sqrt{54}cm\]
D) \[\sqrt{930}cm\]

Answer 1

Hint:
In order to solve the given question, first we will draw the two altitudes from A to the line CD at the point P and the other is from B to the line CD at the point Q. Then find out the length of QC by using the Pythagoras theorem, we will now get which one diagonal is longer form the two diagonal and then by using Pythagoras theorem we will get the length of the longer diagonal.

Complete step by step solution:
We have given that,
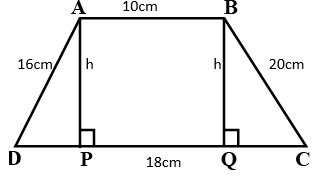
ABCD is a trapezium of side measures 10 cm, 20 cm, 18 cm and 16 cm.

Now,
Draw the two altitudes from A to the line CD at the point P and the other is from B to the line CD at the point Q.
We have now two right-angled triangles \[\Delta APD\] and \[\Delta BQC\].
\[\Delta BQC\]Has sides ‘x’ cm, ‘h’ cm and 20 cm.
\[\Delta APD\]Has sides ‘x - 8’ cm, ‘h’ cm and 16 cm.
Now, taking the triangle \[\Delta BQC\],
Applying the Pythagoras theorem, i.e. \[{{\left( perpendicular \right)}^{2}}+{{\left( base \right)}^{2}}={{\left( hypotenuse \right)}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{h}^{2}}={{\left( 20 \right)}^{2}}\]
Simplifying the above, we get
\[\Rightarrow {{x}^{2}}+{{h}^{2}}=400\]--------- (1)
Now, taking the triangle\[\Delta APD\],
Applying the Pythagoras theorem, i.e. \[{{\left( perpendicular \right)}^{2}}+{{\left( base \right)}^{2}}={{\left( hypotenuse \right)}^{2}}\]
\[\Rightarrow {{\left( x-8 \right)}^{2}}+{{h}^{2}}={{\left( 16 \right)}^{2}}\]
Expanding the above, we get
\[\Rightarrow {{x}^{2}}-16x+{{8}^{2}}+{{h}^{2}}=256\]
Simplifying the above we get,
\[\Rightarrow {{x}^{2}}+{{h}^{2}}+16x=192\]--------- (2)
Subtracting equation (1) from equation (2), we get
\[\Rightarrow {{x}^{2}}+{{h}^{2}}+16x-\left( {{x}^{2}}+{{h}^{2}} \right)=192-400\]
\[\Rightarrow {{x}^{2}}+{{h}^{2}}+16x-{{x}^{2}}-{{h}^{2}}=-208\]
\[\Rightarrow 16x=-208\]
\[\Rightarrow x=13\]
(As the side of the triangle can never be negative.)
Therefore,
\[\Rightarrow QC=13cm\]
Then,
\[\Rightarrow QD=18cm-13cm=5cm\]
So we can said that,
Longer diagonal must be AC rather than BD.
Now, taking the triangle \[\Delta APC\], where AC = d, AP = h and PC = 10 + 13 = 23cm.
\[\Rightarrow {{d}^{2}}={{h}^{2}}+{{\left( 23 \right)}^{2}}\]
Simplifying the above, we get
\[\Rightarrow {{d}^{2}}=\left( 400-169 \right)+529=231+529=760\]
Transposing the power 2 to the RHS, we get
\[\Rightarrow d=\sqrt{760}cm\]
Therefore,
The measure of the longer diagonal will be \[\sqrt{760}cm\].

Hence, the option (a) will be the correct answer.

Note:
In order to solve the given question, students need to know about the concept of trapezium and its properties. A trapezium of a quadrilateral having four sides from then two parallel sides of unequal length and the other two are the non-parallel sides. The parallel sides of the trapezium are also said bases and the other non-parallel sides of the given trapezium is said to be the legs of the trapezium. Trapezium can also be known as trapezoid.