Question

If the two opposite vertices of a square are $\left( -1,2 \right)$ and $\left( 3,2 \right)$, then find the coordinates of the other two vertices?
(a) $\left( 1,4 \right)$ and $\left( -1,1 \right)$.
(b) $\left( 1,4 \right)$ and $\left( 1,0 \right)$,
(c) $\left( 1,-4 \right)$ and $\left( 1,1 \right)$,
(d) $\left( 1,-4 \right)$ and $\left( 1,0 \right)$.

Answer 1

Hint: We start solving the problem by assigning the variables for the vertices of the square and drawing all the given information. We then assume a point for the third vertex and use the fact that the lengths of all sides of a square are equal. Using this fact, we find the x coordinate for the other two points. We then find the length of the side of the square using the fact that the distance between the two opposite sides in a square is equal to the $\sqrt{2}$ times of the length of the side of the square. We use this length of the side and find the y coordinates of the other two vertices.

Complete step-by-step answer:
According to the problem, the two opposite vertices of a square are $\left( -1,2 \right)$ and $\left( 3,2 \right)$. We need to find the coordinates of the remaining two vertices. Let us assume the square be ABCD and the gives vertices as A and C.
Let us assume one of the other vertices is $\left( x,y \right)$. Let us draw the given information to get a better view.

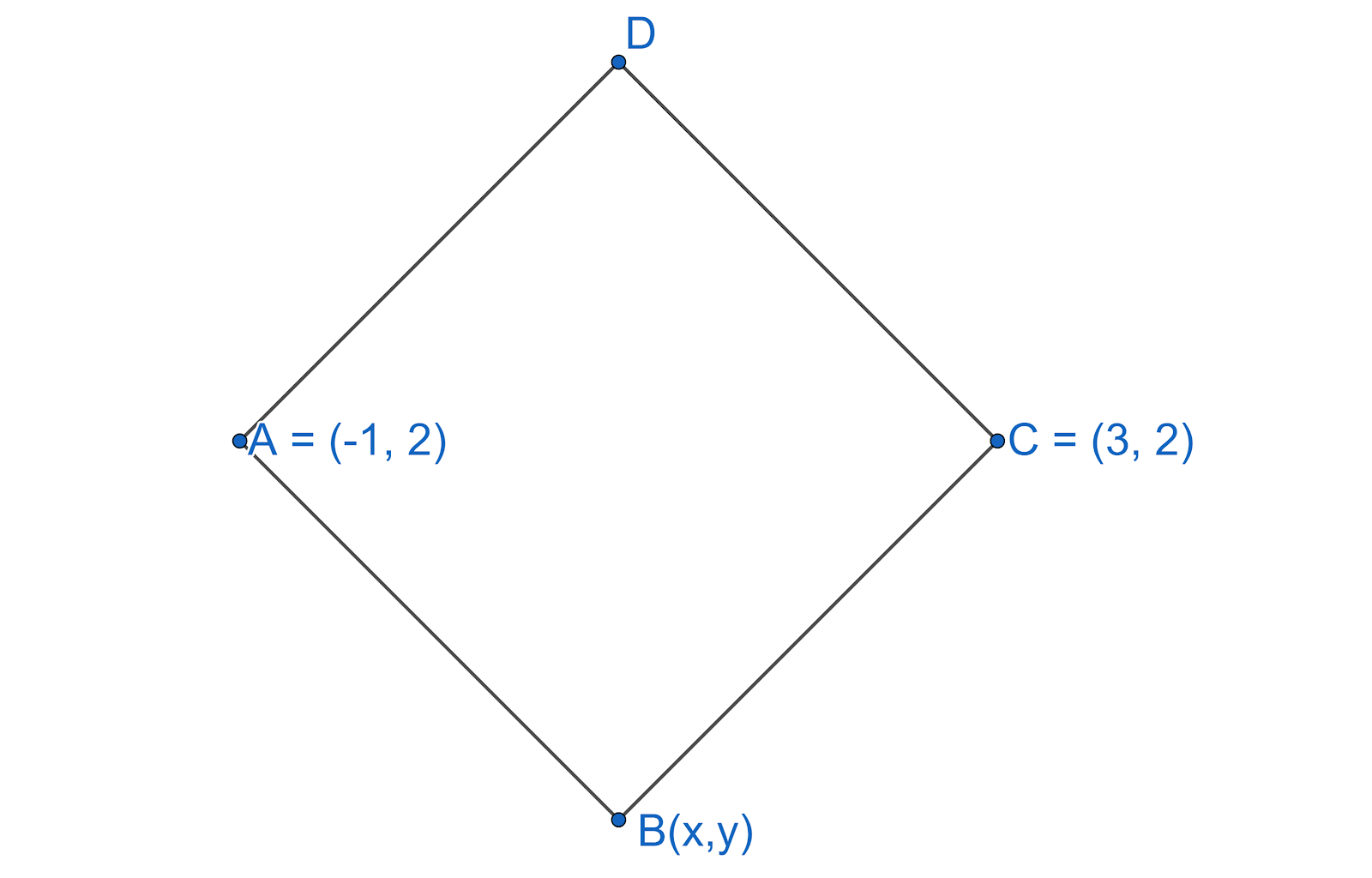
We know that the length of the sides in a square are equal. From the figure, we can see that the length of the sides AB and BC are equal.
We know that the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.
So, we have $AB=BC$. We square these lengths on both sides.
\[\Rightarrow A{{B}^{2}}=B{{C}^{2}}\].
\[\Rightarrow {{\left( \sqrt{{{\left( x-\left( -1 \right) \right)}^{2}}+{{\left( y-2 \right)}^{2}}} \right)}^{2}}={{\left( \sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}} \right)}^{2}}\].
\[\Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}\].
We cancel the terms that were the same on both sides.
\[\Rightarrow {{\left( x+1 \right)}^{2}}={{\left( x-3 \right)}^{2}}\].
\[\Rightarrow {{x}^{2}}+2x+1={{x}^{2}}-6x+9\].
\[\Rightarrow 2x+6x=9-1\].
\[\Rightarrow 8x=8\].
\[\Rightarrow x=1\].
∴ The value of the x coordinate is 1.
We know that the distance between the two opposite sides in a square is equal to the $\sqrt{2}$ times of the length of the side of the square. Let us assume the length of the side of the square be a.
So, we have $\sqrt{2}a=\sqrt{{{\left( -1-3 \right)}^{2}}+{{\left( 2-2 \right)}^{2}}}$.
$\Rightarrow \sqrt{2}a=\sqrt{{{\left( 4 \right)}^{2}}+0}$.
$\Rightarrow \sqrt{2}a=4$, as length cannot be negative.
$\Rightarrow a=2\sqrt{2}m$.
So, we have the length of the side of the square as $2\sqrt{2}m$.
So, we have $BC=2\sqrt{2}m$.
\[\Rightarrow \sqrt{{{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}}=2\sqrt{2}\].
\[\Rightarrow {{\left( 1-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{\left( 2\sqrt{2} \right)}^{2}}\].
\[\Rightarrow {{\left( -2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=8\].
\[\Rightarrow 4+{{\left( y-2 \right)}^{2}}=8\].
\[\Rightarrow {{\left( y-2 \right)}^{2}}=4\].
\[\Rightarrow \left( y-2 \right)=\pm 2\].
\[\Rightarrow y-2=2\] or $y-2=-2$.
\[\Rightarrow y=4\] or $y=0$.
So, the coordinates of the other two vertices of the square are $\left( 1,4 \right)$ and (1,0), as $\left( x,y \right)$ represents the locus of the point on the square the other value of y will be coordinate for other vertex.
The correct option for the given problem is (b).

So, the correct answer is “Option (b)”.

Note: We can see that the equation of the diagonal joining the points A and C is parallel to y-axis. We know that the diagonals are perpendicular to each other in square. So, the other diagonal should be parallel to x-axis. This tells us that the x-coordinate of both the points are the same. We can also check this using the midpoint of the diagonal as the diagonals bisect each other in a square.