Question

If the value of \[\tan \alpha =\dfrac{5}{12}\] , find all other trigonometric ratios.

Answer 1

Hint: In this question, we are given the value of \[\tan \alpha \] and we are asked to find all other trigonometric ratios. We have to find all the trigonometric ratios, step by step. We know the identity, \[{{\sec }^{2}}\alpha -{{\tan }^{2}}\alpha =1\] . Using this relation, \[\sec \alpha \] can be obtained. And using the value of \[\sec \alpha \] , \[\cos \alpha \] can be calculated. We also know the identity, \[{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\]. Using this identity, \[\sin \alpha \] can be calculated. Now, we have the value of \[\sin \alpha \] and \[\cos \alpha \] . Using the value of \[\sin \alpha \] and \[\cos \alpha \] , \[\tan \alpha \] can be calculated. Now, other remaining trigonometric ratios can be calculated by finding the reciprocal of these trigonometric ratios.

Complete step-by-step answer:
Now, according to the question, it is given that \[\tan \alpha =\dfrac{5}{12}\]………………….(1)

We know that, \[{{\sec }^{2}}\alpha -{{\tan }^{2}}\alpha =1\] ……………………(2)

Taking \[{{\tan }^{2}}\alpha \] to the RHS in the equation (2), we get

\[{{\sec }^{2}}\alpha =1+{{\tan }^{2}}\alpha \]…………….(3)

Now, \[\sec \alpha \] can be easily expressed in terms of \[\tan \alpha \] .

Taking square root in both LHS and RHS in equation (3), we get

\[\sec \alpha =\sqrt{1+{{\tan }^{2}}\alpha }\]……………….(4)

In question, we are given the value of \[\tan \alpha \] . Putting the value of \[\tan \alpha \]

from equation (1) in equation (4), we get

\[\begin{align}

  & \sec \alpha =\sqrt{1+{{\left( \dfrac{5}{12} \right)}^{2}}} \\

 & \Rightarrow \sec \alpha =\sqrt{1+\dfrac{25}{144}} \\

 & \Rightarrow \sec \alpha =\sqrt{\dfrac{144+25}{144}} \\

 & \Rightarrow \sec \alpha =\sqrt{\dfrac{169}{144}} \\

 & \Rightarrow \sec \alpha =\dfrac{13}{12} \\

\end{align}\]

Now, we have

\[sec\alpha =\dfrac{13}{12}\]……………….(5)

From equation (1) and equation (5), we have got the values of \[\sec \alpha \] and \[\tan \alpha \] .

Using equation (5), we can find the value of \[\cos \alpha \] .

We know that,

\[\dfrac{1}{sec\alpha }=\cos \alpha\]…………………….(6)

Putting the values of \[\sec \alpha \] in equation (6), we get

\[\begin{align}

  & \cos \alpha =\dfrac{1}{\sec \alpha } \\

 & \Rightarrow \cos \alpha =\dfrac{1}{\dfrac{13}{12}} \\

 & \Rightarrow \cos \alpha =\dfrac{12}{13} \\

\end{align}\]

Now, we also have

\[\cos \alpha =\dfrac{12}{13}\]………………..(7)

We have to find other remaining trigonometric ratios that are \[\sin \alpha \], \[\cos ec\alpha \] , and \[\cot \alpha \] .

We know the identity,

\[{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\]……………………(8)

Taking \[{{\sin }^{2}}\alpha \] to the RHS in the equation (8), we get

\[{{\sin }^{2}}\alpha =1-{{\cos }^{2}}\alpha \]…………….(9)

Now, \[\sin \alpha \] can be easily expressed in terms of \[\cos \alpha \] .

Taking square root in both LHS and RHS in equation (9), we get

\[sin\alpha =\sqrt{1-{{\cos }^{2}}\alpha }\]……………(10)

In equation(7), we have got the value of \[\cos \alpha \]. Putting the value of \[\cos \alpha \]

from equation (7) in equation (10), we get

\[\begin{align}

  & sin\alpha =\sqrt{1-co{{s}^{2}}\alpha } \\

 & \Rightarrow sin\alpha =\sqrt{1-{{\left( \dfrac{12}{13} \right)}^{2}}} \\

 & \Rightarrow sin\alpha =\sqrt{1-\dfrac{144}{169}} \\

 & \Rightarrow sin\alpha =\sqrt{\dfrac{169-144}{169}} \\

 & \Rightarrow sin\alpha =\sqrt{\dfrac{25}{169}} \\

 & \Rightarrow sin\alpha =\dfrac{5}{13} \\

\end{align}\]

We know that \[\sec \alpha \] , \[\operatorname{cosec}\alpha \] , and \[\cot \alpha \] is reciprocal of \[\cos \alpha \], \[\sin \alpha \] and \[\tan \alpha \]respectively.

\[\begin{align}

  & \sin \alpha =\dfrac{5}{13}, \\

 & \cos ec\alpha =\dfrac{1}{\sin \alpha }=\dfrac{13}{5}. \\

\end{align}\]

\[\begin{align}

  & \cos \alpha =\dfrac{12}{13}, \\

 & sec\alpha =\dfrac{1}{cos\alpha }=\dfrac{13}{12}. \\

\end{align}\]

\[\begin{align}

  & tan\alpha =\dfrac{5}{12}, \\

 & \cot \alpha =\dfrac{1}{tan\alpha }=\dfrac{12}{5}. \\

\end{align}\]

Now, we have got all the trigonometric ratios.


Note: This question can also be solved by using the Pythagoras theorem.

We have, \[\tan \alpha =\dfrac{5}{12}\] .

Now, using a right-angled triangle, we can get the value of \[\cos \alpha \].

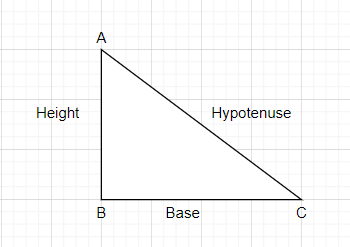
Using Pythagoras theorem, we can find the hypotenuse.

Hypotenuse = \[\sqrt{{{\left( base \right)}^{2}}+{{\left( height \right)}^{2}}}\]

\[\begin{align}

  & \sqrt{{{\left( 12 \right)}^{2}}+{{(5)}^{2}}} \\

 & =\sqrt{144+25} \\

 & =\sqrt{169} \\

 & =13 \\

\end{align}\]

\[\begin{align}

  & \cos \alpha =\dfrac{base}{hypotenuse} \\

 & \cos \alpha =\dfrac{12}{13} \\

\end{align}\]

We know that,

\[\sin \alpha =\dfrac{height}{hypotenuse}\]

\[\sin \alpha =\dfrac{5}{13}\]

Now, other remaining trigonometric ratios can be calculated by finding the reciprocal of these trigonometric ratios.