Question

If the vertices of a hyperbola be at $\left( -2,0 \right)$, $\left( 2,0 \right)$ and one of its foci be at $\left( -3,0 \right)$, then which of the following points does not lie on hyperbola?
(a) $\left( 4,\sqrt{15} \right)$,
(b) $\left( -6,2\sqrt{10} \right)$,
(c) $\left( 6,5\sqrt{2} \right)$,
(d) $\left( 2\sqrt{2},\sqrt{5} \right)$.

Answer 1

Hint: We start solving the problem by finding the centre of the hyperbola using the fact that the centre of the hyperbola lies at the midpoint of the line segment joining two vertices. We then write the general equation of the hyperbola and then compare the general of vertices with the given ones to find the length of the major axis. We then use the general point for the foci and compare it with the given point to find the eccentricity. We find the length of the minor axis by using the value of eccentricity. We get an equation of parabola in which we substitute points and verify them to get the required point.

Complete step by step answer:
We have given that $\left( -2,0 \right)$, $\left( 2,0 \right)$ are vertices of hyperbola and $\left( -3,0 \right)$ is one of its foci. We need to find the point from the options that doesn’t lie on hyperbola.
Let us draw to get a better view.

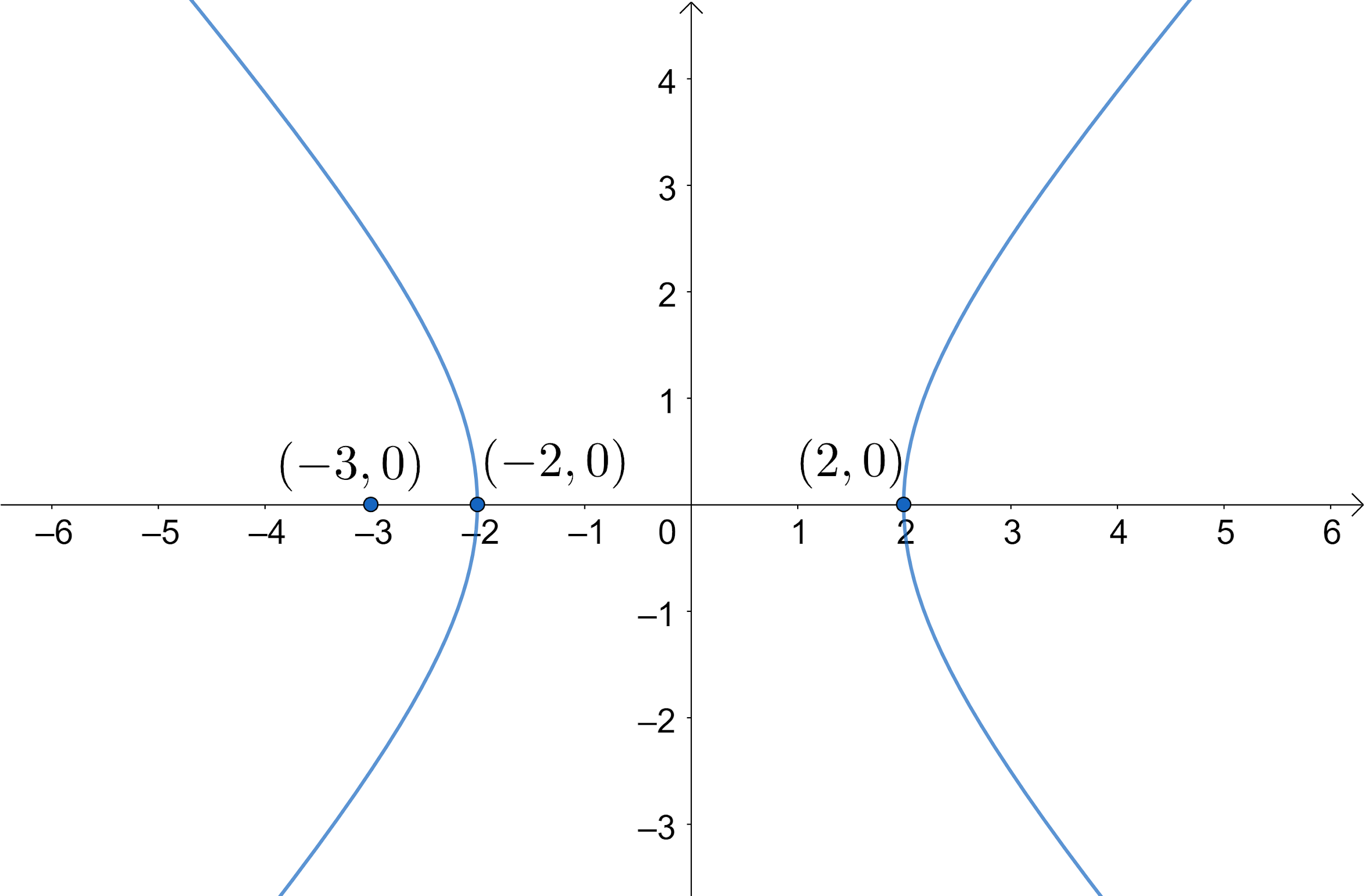
We know that the centre of the hyperbola lies at the midpoint of the line segment joining two vertices. So, the centre is the midpoint of $\left( -2,0 \right)$ and $\left( 2,0 \right)$.
$\Rightarrow $centre = $\left( \dfrac{-2+2}{2},\dfrac{0+0}{2} \right)$.
$\Rightarrow $centre = $\left( \dfrac{0}{2},\dfrac{0}{2} \right)$.
$\Rightarrow $centre = $\left( 0,0 \right)$.
We know that the general equation of the hyperbola is $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ ---(1), where ${{a}^{2}}>{{b}^{2}}$.
We know that the vertices of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ are $\left( \pm a,0 \right)$ ---(2).
According to the problem, the vertices are $\left( \pm 2,0 \right)$. Comparing this with equation (2) we get $a=2$.
So, we have ${{a}^{2}}=4$. Let us substitute this value in equation (1) which makes the equation of the hyperbola as $\dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$.
We know that the general form of the foci of hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is $\left( \pm ae,0 \right)$ ---(3), where ‘e’ is eccentricity of the ellipse.
According to the problem, we have given that one of the foci is $\left( -3,0 \right)$. Comparing equation (3), we get $ae=3$ as the values of ‘a’ and ‘e’ are positive.
We have $ae=3$.
$\Rightarrow 2e=3$.
$\Rightarrow e=\dfrac{3}{2}$ ---(4).
We know that the eccentricity of the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ is $e=\dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}$. We use this in equation (4).
$\Rightarrow \dfrac{\sqrt{{{a}^{2}}+{{b}^{2}}}}{a}=\dfrac{3}{2}$.
$\Rightarrow \dfrac{\sqrt{{{2}^{2}}+{{b}^{2}}}}{2}=\dfrac{3}{2}$.
$\Rightarrow \sqrt{4+{{b}^{2}}}=3$.
$\Rightarrow 4+{{b}^{2}}={{3}^{2}}$.
$\Rightarrow 4+{{b}^{2}}=9$.
$\Rightarrow {{b}^{2}}=9-4$.
$\Rightarrow {{b}^{2}}=5$. We substitute this in equation (1)
The equation of hyperbola is $\dfrac{{{x}^{2}}}{4}-\dfrac{{{y}^{2}}}{5}=1$ ---(5).
Let us substitute each point in equation (5) and check whether they are satisfying this or not.
We have option (a) as $\left( 4,\sqrt{15} \right)$.
$\Rightarrow \dfrac{{{4}^{2}}}{4}-\dfrac{{{\left( \sqrt{15} \right)}^{2}}}{5}=1$.
$\Rightarrow \dfrac{16}{4}-\dfrac{15}{5}=1$.
$\Rightarrow 4-3=1$.
$\Rightarrow 1=1$. This point lies on the hyperbola as we get the same R.H.S and L.H.S.
We have option (b) as $\left( -6,2\sqrt{10} \right)$.
$\Rightarrow \dfrac{{{\left( -6 \right)}^{2}}}{4}-\dfrac{{{\left( 2\sqrt{10} \right)}^{2}}}{5}=1$.
$\Rightarrow \dfrac{36}{4}-\dfrac{40}{5}=1$.
$\Rightarrow 9-8=1$.
$\Rightarrow 1=1$. This point lies on the hyperbola as we get the same R.H.S and L.H.S.
We have option (c) as $\left( 6,5\sqrt{2} \right)$.
$\Rightarrow \dfrac{{{\left( 6 \right)}^{2}}}{4}-\dfrac{{{\left( 5\sqrt{2} \right)}^{2}}}{5}=1$.
$\Rightarrow \dfrac{36}{4}-\dfrac{50}{5}=1$.
$\Rightarrow 9-10=1$.
$\Rightarrow -1=1$. This point does not lie on the hyperbola as we got different R.H.S and L.H.S.
We have option (d) as $\left( 2\sqrt{2},\sqrt{5} \right)$.
$\Rightarrow \dfrac{{{\left( 2\sqrt{2} \right)}^{2}}}{4}-\dfrac{{{\left( \sqrt{5} \right)}^{2}}}{5}=1$.
$\Rightarrow \dfrac{8}{4}-\dfrac{5}{5}=1$.
$\Rightarrow 2-1=1$.
$\Rightarrow 1=1$. This point lies on the hyperbola as we get the same R.H.S and L.H.S.
We have found that the point $\left( 6,5\sqrt{2} \right)$ does not lie on hyperbola.

So, the correct answer is “Option C”.

Note: We should not assume the equation of hyperbola without finding the centre. We can also find the distance between the nearby vertex to the given foci to get the eccentricity of hyperbola. We can use a parametric equation for the points to check the points which requires precise calculation. We should know that if the hyperbola touches any x-axis, then it will be asymptotic to the other axis. Similarly, we can expect problems which have conics like ellipse, parabola, circle and straight lines.