Question

If two sides and a median bisecting one of these sides of a triangle are respectively proportional to the two sides and the corresponding median of another triangle, then prove that triangles are similar.

Answer 1

Hint: First, we have drawn two triangles of different size. Then, we have to prove that two triangles are similar using side angle side (SAS) criterion. So, we will first prove that sides of $\Delta ABE\sim \Delta PQL$ are equal using the concept of side side side (SSS) criterion. Then, we will prove that $\angle CAB=\angle RPQ$ . So, here we will prove that the triangle is similar using SAS criterion.

Complete step by step solution:
Now, we take two triangles i.e. $\Delta ABC,\Delta PQR$ and median will be AD and PM as shown in the below figure.
 

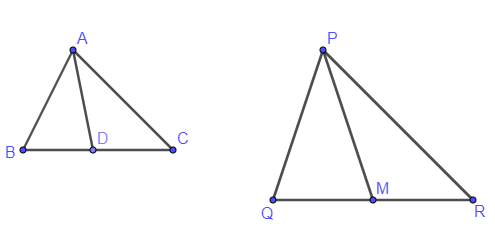
Now, let us extend AD to point E such that $AD=DE$ and PM up to point L such that $PM=ML$ .
Then, we will join B to E, C to E, Q to L and R to L.

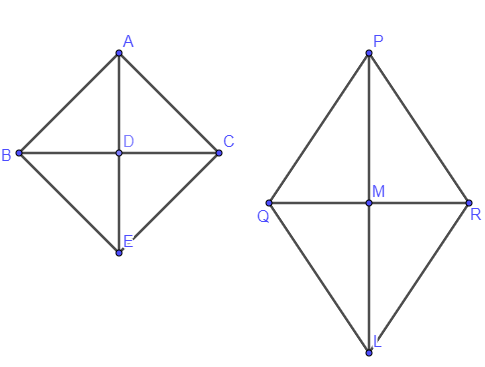
We know that medians are the bisector of the opposite side. Thus, we can write as $BD=DC$ .
Also, $AD=DE$ . In quadrilateral ABEC, diagonals AE and BC bisect each other at point D.
Therefore, ABEC is a parallelogram.
Since, we know that opposite sides of parallelograms are equal. So, we can write as
$AC=BE$ and $AB=EC$ ……………………………(1)
Similarly, we know that medians are the bisector of the opposite side so, $QM=MR$
Also, $PM=ME$ . In quadrilateral PQER, diagonals PL and QR bisect each other at point M.
Therefore, PQER is a parallelogram.
Since, we know that opposite sides of parallelograms are equal. So, we can write as
$PR=RL$ and $PQ=QL$ ……………………………………(2)
Now, we are given that if two sides and a median bisecting one of these sides of a triangle are respectively proportional to the two sides and the corresponding median of another triangle. So, in mathematical form, we can write it as
$\dfrac{AB}{PQ}=\dfrac{AC}{PR}=\dfrac{AD}{PM}$
So, from equation (1) and (2), we can write is as
$\dfrac{AB}{PQ}=\dfrac{BE}{QL}=\dfrac{AD}{PM}$
Now, we know that 2AD will be equal to AE i.e. $AE=AD+DE$ which we know $AD=DE$ . Same for 2PM will be equal to $PL$ i.e. $PL=PM+ML$ which we know $PM=ML$ .
So, multiplying and dividing 2 in the equation, we get
$\dfrac{AB}{PQ}=\dfrac{BE}{QL}=\dfrac{2AD}{2PM}$
$\dfrac{AB}{PQ}=\dfrac{BE}{QL}=\dfrac{AE}{PL}$ ………………………….(3)
Thus, $\Delta ABE$ and $\Delta PQL$ are similar by SSS criteria denoted as $\Delta ABE\sim \Delta PQL$ .
Similarly, we can say that $\Delta ACE\sim \Delta PRL$ by SSS criteria.
Now, we know that corresponding angles of similar triangles are equal. So, we can write it as
$\angle BAE=\angle QPL$ …………………….(4)
$\angle CAE=\angle RPL$ ………………….(5)
On adding equation (3) and (4), we get
$\angle BAE+\angle CAE=\angle QPL+\angle RPL$
Thus, we can see in the figure that $\angle BAE+\angle CAE=\angle CAB$ and $\angle QPL+\angle RPL=\angle RPQ$ . So, on substituting these values, we get
$\angle CAB=\angle RPQ$ ………………………………………(6)
Therefore, in $\Delta ABC$ and $\Delta PQR$ , we can say that $\dfrac{AB}{PQ}=\dfrac{AC}{PR}$ and $\angle CAB=\angle RPQ$ .
Thus, we have proved two sides and one angle is equal using side angle side (SAS) similarity criterion.
Hence, proved.

Note: In this type of problem, clear understanding of diagonals and bisector students should have. Then only this theory-based question will be easily solved. Also, remember in the SAS theorem, the angle between any two sides should be proved similar to another triangle. Do not take any two random sides and angle the third side which is not in between two sides. This will lead to wrong answers. So, do have a clear concept regarding SAS criterion.