Question

If two tablets of disprin of $1.2{\text{ g}}$ each are dissolved in $1{\text{ litre}}$ of water then calculate the pH of resultant aqueous solution. [Given: Disprin consists $75\% $ of aspirin acid, ${K_a}$ of aspirin is ${10^{ - 2}}$]

A) 1.1
B) 2.2
C) 3.3
D) 4.4

Answer 1

Hint: To solve this first calculate the actual concentration of aspirin acid in disprin. The concentration of aspirin acid will be equal to the concentration of hydrogen ion in the aqueous solution of disprin. Then from the concentration of hydrogen ion calculate the pH. Remember that aspirin acid is a weak acid.


Complete solution:
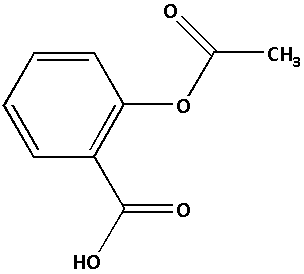
We are given that disprin consists of $75\% $ of aspirin acid. And two tablets of disprin of $1.2{\text{ g}}$ each are dissolved in $1{\text{ litre}}$ of water. Thus,
Amount of aspirin acid present in a $1.2{\text{ g}}$ tablet of disprin $ = \dfrac{{75}}{{100}} \times 1.2{\text{ g}}$
Amount of aspirin acid present in a $1.2{\text{ g}}$ tablet of disprin $ = 0.9{\text{ g}}$
Now, $1.2{\text{ g}}$ tablet of disprin is dissolved in $1{\text{ litre}}$ of water. Thus,
Concentration of aspirin acid $ = \dfrac{{{\text{0}}{\text{.9 g}}}}{{1{\text{ L}}}}$
Concentration of aspirin acid $ = {\text{0}}{\text{.9 M}}$
The concentration of aspirin acid is equal to the concentration of hydrogen ion in the aqueous solution of disprin. Thus,
Concentration of hydrogen ion $ = {\text{0}}{\text{.9 M}}$
Calculate the $p{K_a}$ of aspirin acid using the equation as follows:
$p{K_a} = - \log {K_a}$
Where ${K_a}$ is the dissociation constant of acid.
We are given that ${K_a}$ of aspirin acid is ${10^{ - 2}}$. Thus,
$p{K_a} = - \log \left( {{{10}^{ - 2}}} \right)$
$p{K_a} = 2$
The equation to calculate the pH of a weak acid is as follows:
${\text{pH}} = \dfrac{1}{2}\left( {p{K_a} - \log C} \right)$
Where $C$ is the concentration of the weak acid.
Substitute 2 for the $p{K_a}$ of aspirin acid, ${\text{0}}{\text{.9 M}}$ for the concentration of aspirin acid. Thus,
${\text{pH}} = \dfrac{1}{2}\left( {2 - \log \left( {{\text{0}}{\text{.9 M}}} \right)} \right)$
${\text{pH}} = \dfrac{1}{2}\left( {2 - \left( { - {\text{0}}{\text{.04575}}} \right)} \right)$
${\text{pH}} = \dfrac{1}{2}\left( {2.04575} \right)$
${\text{pH}} = 1.02 \approx 1.1$
Thus, the pH of resultant aqueous solution is 1.1.

Thus, the correct option is (A) 1.1.


Note:If the pH is less than 7 then the solution is acidic. If the pH is more than 7 then the solution is basic or alkaline. If the pH is equal to 7 then the solution is neutral. Here the pH of the solution of disprin is 1.1 which means that the solution is acidic in nature.