Question

If Y-axis is the directrix of the ellipse with eccentricity $e = \dfrac{1}{2}$ and the corresponding focus is at (3,0), find the equation to its auxiliary circle.
$
  {\text{A}}{\text{. }}{x^2} + {y^2} - 8x + 12 = 0 \\
  {\text{B}}{\text{. }}{x^2} + {y^2} - 8x - 12 = 0 \\
  {\text{C}}{\text{. }}{x^2} + {y^2} - 8x + 9 = 0 \\
  {\text{D}}{\text{. }}{x^2} + {y^2} = 4 \\
$

Answer 1

Hint- Here, we will proceed by using the formulas for the equation of directrix i.e.,$x = h - \dfrac{a}{e}$ , the focus coordinates i.e., F(h-ae,k) and ${b^2} = {a^2}\left( {1 - {e^2}} \right)$ corresponding to any ellipse $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$ where a>b.

Complete step by step answer:

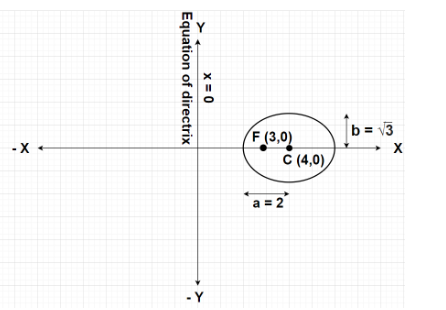
Given, Directrix to the given ellipse is represented by equation of Y-axis i.e., x = 0
Eccentricity, $e = \dfrac{1}{2}$
Focus of the ellipse is at F(3,0)
Since, the directrix of the given ellipse lies along the Y-axis. Therefore, the ellipse will be oriented along the X-axis.
Let the equation of the ellipse along Y-axis is given by $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1{\text{ }} \to {\text{(1)}}$ where a>b and the centre of the ellipse lies at point C(h,k).
As we know that the equation of the directrix to any ellipse $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$ (having eccentricity as e) where a>b is given by
$x = h - \dfrac{a}{e}$
For the given ellipse, equation of the directrix is x = 0
$
   \Rightarrow 0 = h - \dfrac{a}{e} \\
   \Rightarrow h = \dfrac{a}{e} \\
 $
By putting $e = \dfrac{1}{2}$ in the above equation, we get
$
   \Rightarrow h = \dfrac{a}{{\left( {\dfrac{1}{2}} \right)}} \\
   \Rightarrow h = 2a{\text{ }} \to {\text{(2)}} \\
 $
Also, the focus coordinates for any ellipse $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$ (having eccentricity as e) where a>b is given by F(h-ae,k)
Also, focus of the given ellipse is F(3,0)
So, h-ae = 3
$
   \Rightarrow 2a - a\left( {\dfrac{1}{2}} \right) = 3 \\
   \Rightarrow 2a - \dfrac{a}{2} = 3 \\
   \Rightarrow \dfrac{{4a - a}}{2} = 3 \\
   \Rightarrow \dfrac{{3a}}{2} = 3 \\
   \Rightarrow a = 2 \\
 $
Hence, ${a^2} = {2^2} = 4$
Also, k = 0
Using the formula ${b^2} = {a^2}\left( {1 - {e^2}} \right)$, the value of ${b^2}$ is given as
$
   \Rightarrow {b^2} = 4\left( {1 - {{\left( {\dfrac{1}{2}} \right)}^2}} \right) = 4\left( {1 - \dfrac{1}{4}} \right) = 4\left( {\dfrac{{4 - 1}}{4}} \right) = 4\left( {\dfrac{3}{4}} \right) \\
   \Rightarrow {b^2} = 3 \\
 $
Putting a = 2 in equation (2), we get
$ \Rightarrow h = 2 \times 2 = 4$
Putting ${a^2} = 4$, ${b^2} = 3$, h = 4 and k = 0 in equation (1), we get
$
   \Rightarrow \dfrac{{{{\left( {x - 4} \right)}^2}}}{4} + \dfrac{{{{\left( {y - 0} \right)}^2}}}{3} = 1 \\
   \Rightarrow \dfrac{{{{\left( {x - 4} \right)}^2}}}{4} + \dfrac{{{y^2}}}{3} = 1 \\
 $
This above equation represents the equation of the given ellipse.
Equation of the auxiliary circle to the ellipse $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$ where a>b is given by
${\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {a^2}{\text{ }} \to {\text{(3)}}$
By putting ${a^2} = 4$, h = 4 and k = 0 in the equation (3), we get
$
   \Rightarrow {\left( {x - 4} \right)^2} + {\left( {y - 0} \right)^2} = 4 \\
   \Rightarrow {\left( {x - 4} \right)^2} + {y^2} = 4 \\
   \Rightarrow {x^2} + {4^2} - 8x + {y^2} = 4 \\
   \Rightarrow {x^2} + {y^2} - 8x + 12 = 0 \\
 $
The above equation represents the required equation of the auxiliary circle to the given ellipse.
Hence, option A is correct.

Note- In this particular problem, firstly it very important to find out that the given ellipse corresponds to which one of the two general cases of ellipse i.e., $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$ where a>b or $\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1$ where b>a, in order to use the formulas for various parameters. Also, the major axis of the given ellipse is X-axis and the minor axis is Y-axis.