Question

In a circle of diameter 40 cm the length of a chord is 20 cm. Find the length of the minor arc of the chord.

Answer 1

- Hint: Let us draw the diagram first to understand the given problem,

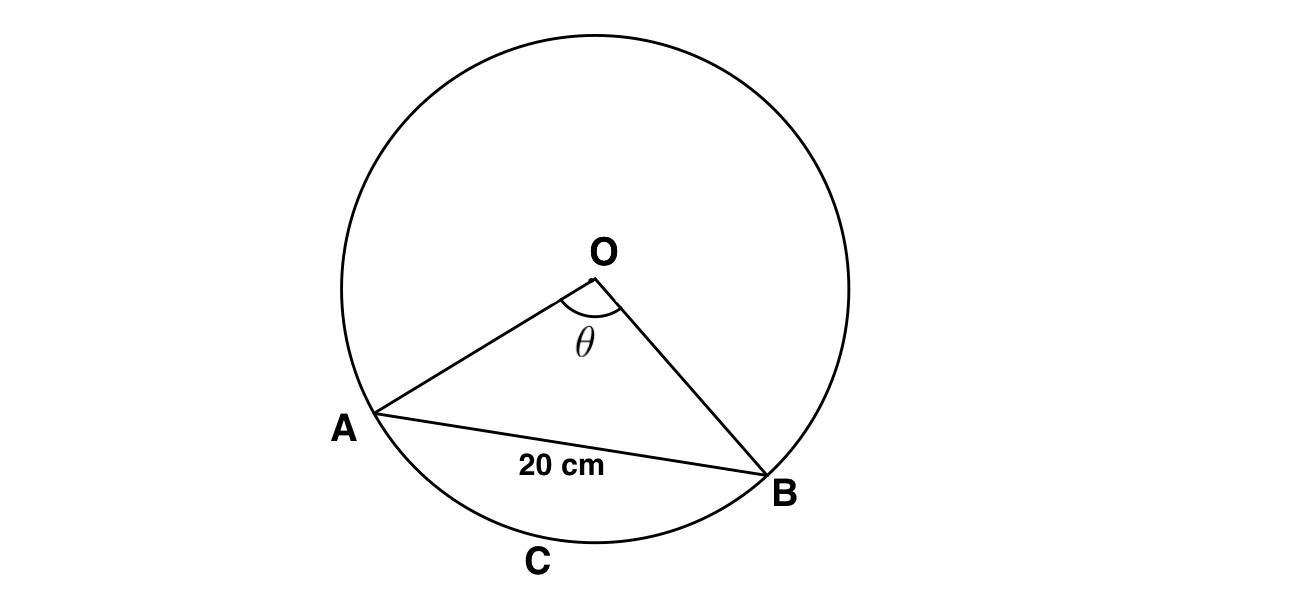
Here it is given a circle of diameter 40 cm and the length of a chord AB is 20 cm. Then we have to find the length of the minor arc ACB of the chord AB. So to find the solution we first need to find the measure of the angle $$\angle AOB$$ and after that by using the below formula we can easily find the length of the arcABC.
The formula states that, if we know the radius of a circle is r unit and an arc of length I unit subtends an angle θ radian at the centre, then $$l=r\theta$$.......(1)

Complete step-by-step solution -
Given, diameter of the circle =40 cm
Therefore the radius(r) = $$\dfrac{40}{2} \ cm\ =20\ cm$$
Now Since OB and OC are the radius of the circle,
$$\therefore$$ From the diagram we can say that OB = OC = 20 cm
Let AB be a chord of length = 20 cm of the given circle.
$$\therefore$$ AB = 20 cm
So from the diagram we can say that $$\triangle AOC$$ is an equilateral triangle, and as we know that for an equilateral triangle all the angles are $$60^{\circ }$$.
Therefore, $$\theta =60^{\circ }$$
Which also can be written as, $$\theta =\dfrac{\pi }{180^{{}\circ }} \times 60^{\circ }\ rad$$ = $$=\dfrac{\pi }{3} \ rad$$
Now by the formula (1) we can write,
$$l=r\times \theta$$
$$\Rightarrow \text{arc} \ ACB=OB\times \theta$$
$$\Rightarrow \text{arc} \ ACB=20\times \dfrac{\pi }{3} \ cm$$
$$\Rightarrow \text{arc} \ ACB=\dfrac{20\pi }{3} \ cm$$
Therefore the length of the minor arc ACB is $$\dfrac{20\pi }{3} \ cm$$

Note: To solve this type of question you need to know that the arc of a circle is defined as the part or segment of the circumference of a circle. A straight line that could be drawn by connecting the two ends of the arc is known as a chord of a circle. If the length of an arc is exactly half of the circle, it is known as a semicircular arc.
Also if you draw one chord then this will generate two arcs, one is called major arc and another one is minor arc.