Question

In a collinear collision, a particle with an initial speed ${{v}_{0}}$ strikes a stationary particle of the same mass. If the final total kinetic of energy is $50%$ greater than the original kinetic energy, the magnitude of the relative velocity between the two particles after collision, is :
\[\begin{align}
  & \text{A}\text{. }\dfrac{{{v}_{0}}}{4} \\
 & \text{B}\text{. }\sqrt{2}{{v}_{0}} \\
 & \text{C}\text{. }\dfrac{{{v}_{0}}}{2} \\
 & \text{D}\text{. }\dfrac{{{v}_{0}}}{\sqrt{2}} \\
\end{align}\]

Answer 1

Hint: As the collision is collinear the conservation of energy and the linear momentum will hold good. So first use the conservation of energy to get a relation between the velocities before collision and velocities after collision. And then use conservation of momentum to get another relation between the velocities before collision and velocities after collision. After that you can calculate the difference between the velocities of the masses after the collision to the relative velocity between the masses.
Formulas used:
The kinetic energy of a particle moving with velocity $v$ and mass $m$ is given by
$K.E=\dfrac{1}{2}m{{v}^{2}}$.
The linear momentum of a particle moving with velocity $v$ and mass $m$ is given by
$P=mv$

Complete step by step answer:

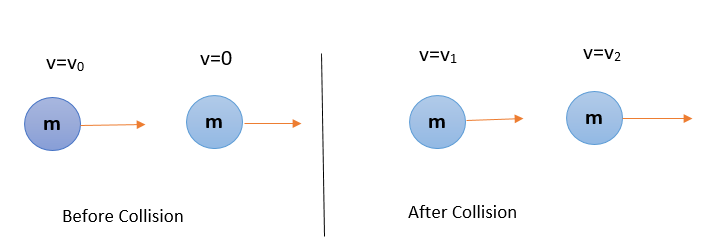
The collision is collinear and the objects are identical. One object is at rest and another is moving with velocity ${{v}_{0}}$ . After the collision the velocities of the two objects are ${{v}_{1}}$ and ${{v}_{2}}$ .
According to the question the final total kinetic of energy is $50%$ greater than the original kinetic energy.
The total Kinetic energy before the collision is $\dfrac{1}{2}mv_{0}^{2}$ and the kinetic energies of the two particles after the collision is $\dfrac{1}{2}mv_{1}^{2}$ and $\dfrac{1}{2}mv_{2}^{2}$.
But the final total kinetic of energy is $50%$ greater than the original kinetic energy. So the $50%$ of the original kinetic energy is \[\dfrac{1}{2}\left( \dfrac{1}{2}mv_{0}^{2} \right)=\dfrac{1}{4}mv_{0}^{2}\] . So according to conservation of kinetic energy
\[\begin{align}
  & \dfrac{1}{2}mv_{0}^{2}+\dfrac{1}{4}mv_{0}^{2}=\dfrac{1}{2}mv_{1}^{2}+\dfrac{1}{2}mv_{2}^{2} \\
 & \Rightarrow \dfrac{3}{4}mv_{0}^{2}=\dfrac{1}{2}mv_{1}^{2}+\dfrac{1}{2}mv_{2}^{2} \\
 & \Rightarrow \dfrac{3}{2}v_{0}^{2}=v_{1}^{2}+v_{2}^{2} \\
 & \Rightarrow v_{1}^{2}+v_{2}^{2}=\dfrac{3}{2}v_{0}^{2} \\
\end{align}\]
The momentum before the collision is $m{{v}_{0}}$ and zero. And the momentum of the objects after the collision is $m{{v}_{1}}$and $m{{v}_{2}}$.
Applying the conservation of momentum
\[\begin{align}
  & m{{v}_{0}}=m{{v}_{1}}+m{{v}_{2}} \\
 & \Rightarrow {{v}_{0}}={{v}_{1}}+{{v}_{2}} \\
 & \Rightarrow v_{0}^{2}={{\left( {{v}_{1}}+{{v}_{2}} \right)}^{2}}=v_{1}^{2}+v_{2}^{2}+2{{v}_{1}}{{v}_{2}} \\
 & \Rightarrow v_{0}^{2}=\dfrac{3}{2}v_{0}^{2}+2{{v}_{1}}{{v}_{2}}\left( \because v_{1}^{2}+v_{2}^{2}=\dfrac{3}{2}v_{0}^{2} \right) \\
 & \Rightarrow 2{{v}_{1}}{{v}_{2}}=v_{0}^{2}-\dfrac{3}{2}v_{0}^{2}=-\dfrac{1}{2}v_{0}^{2} \\
\end{align}\]
Now we calculate the relative velocity of the objects after the collision. i.e. ${{v}_{1}}-{{v}_{2}}$ .
So, ${{\left( {{v}_{1}}-{{v}_{2}} \right)}^{2}}=v_{1}^{2}+v_{2}^{2}-2{{v}_{1}}{{v}_{2}}$
But \[v_{1}^{2}+v_{2}^{2}=\dfrac{3}{2}v_{0}^{2}\] and \[2{{v}_{1}}{{v}_{2}}=-\dfrac{1}{2}v_{0}^{2}\] , now
$\begin{align}
  & {{\left( {{v}_{1}}-{{v}_{2}} \right)}^{2}}=v_{1}^{2}+v_{2}^{2}-2{{v}_{1}}{{v}_{2}}=\dfrac{3}{2}v_{0}^{2}-\left( -\dfrac{1}{2}v_{0}^{2} \right)=\dfrac{3}{2}v_{0}^{2}+\dfrac{1}{2}v_{0}^{2} \\
 & \Rightarrow {{\left( {{v}_{1}}-{{v}_{2}} \right)}^{2}}=\dfrac{4}{2}v_{0}^{2}=2v_{0}^{2} \\
 & \Rightarrow {{v}_{1}}-{{v}_{2}}=\sqrt{2v_{0}^{2}}=\sqrt{2}{{v}_{0}} \\
\end{align}$
Which is the relative velocity after the collision
So the correct option is B.

Note:
The law of conservation of energy states that during elastic collisions the total energy before the collision is equal to the total energy after the collision. It is valid for only elastic collision. Because in elastic collisions no energy is absorbed during the collision. The law of conservation of momentum states that the momentum before the collision is equal to the momentum after the collision.