Question

In a conical pendulum the centripetal force $\left[ {\dfrac{{m{v^2}}}{r}} \right]$ acting on the bob is given by
A. $\dfrac{{mgr}}{{\sqrt {{L^2} - {r^2}} }}$
B. $\dfrac{{mgr}}{{{L^2} - {r^2}}}$
C. $\dfrac{{{{({L^2} - {r^2})}^{\dfrac{1}{2}}}}}{{mgL}}$
D. $\dfrac{{mgL}}{{{{\left( {{L^2} - {r^2}} \right)}^{\dfrac{1}{2}}}}}$

Answer 1

Hint:The concept of free body diagrams are used in order to determine all the forces that are exerted on bob. There are two components of forces that acts on the pendulum which are to be taken into consideration. The basic trigonometric formulae are also applied and are equated to the force components to get an equation for the centripetal force.

Formula used:
The centripetal force of body moving in circular moving with uniform speed is given by:
${F_c} = \dfrac{{m{v^2}}}{r}$
Where, $m$ is the mass of the body, $v$ is the velocity and $r$ is the radius of the circular path.

Complete step by step answer:
A conical pendulum unlike a normal pendulum is one that moves in a circular motion. When a body is moving in a circular motion a force known as the centripetal force is introduced. A centripetal force is a force required to make a body move in a circular path with uniform speed which always tends to act along the radius, towards the center of the circular path. It is given by the following equation:
${F_c} = \dfrac{{m{v^2}}}{r}$ --------($1$)
Where, ${F_c}$ denotes the centripetal force.

Since, the pendulum tends to move about its center point in circles there is a centripetal force associated with it and this force is directed toward the center of the circular path it is moving in. We are asked to find an equation for this centripetal force of the conical pendulum. In order to determine the value of centripetal force, we first need to find out all the forces that are being applied on the bob of the pendulum. This is done easily by using the concept of free body diagrams.

The diagram below illustrates the free body diagram of the conical pendulum:

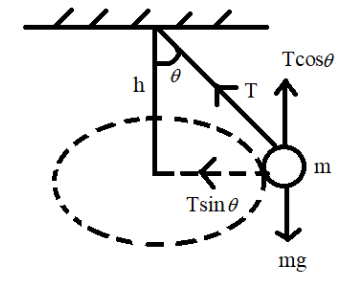
Let us analyze all the forces given from the diagram above. We can see that there are a number of forces that are applied on the bob. Since, the bob has a mass, there will exist a gravitational force acting downwards on the bob given by the equation:
\[F = mg\]

Since, the bob of the pendulum is attached to a string there will be another force that is established which is the tension in the string when the bob is in circular motion. It can be seen that the tension acts at an angle, $\theta $, to the bob. When there is a force that acts at an angle to the body in motion then a set of horizontal and vertical force components are produced from the body in motion.

The horizontal force component is always said to be in terms of sine and the vertical force component directed upwards is said to be in terms of cosine function. These forces come into picture simply by applying the basic trigonometric formulae for sine and cos functions.The variable,$h$ from the above diagram indicates the vertical distance from the center of its circular path. According to the concept of free body diagrams, the upward force exerted on the bob will be equivalent to the downward force on the bob. Hence the following equation is established:
$T\cos \theta = mg$ ------($2$)

The centripetal force that acts on the bob in circular motion in order to balance out the horizontal component of tension and hence another equation is established:
$T\sin \theta = {F_c}$
By substituting equation ($1$) in the above equation we get:
$T\sin \theta = \dfrac{{m{v^2}}}{r}$ -------($3$)
We now divide the equation ($3$) by equation ($2$) to get:
 $\dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{\dfrac{{m{v^2}}}{r}}}{{mg}}$
The common term that is the tension is cancelled out and the equation is simplified further to get:
$\tan \theta = \dfrac{{m{v^2}}}{{mgr}}$ ------- ($4$) [Since, $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$]

Let us now consider a triangle to get the value of $\tan \theta $ in terms of its trigonometric formula. The diagram below shows the triangle ABC:

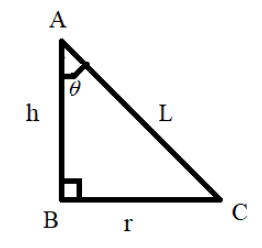
Where, $h$ is the height, $L$ is the length of the string and $r$ is the radius of the circular path.
From the basic trigonometric formula for tan we know that:
$\tan \theta = \dfrac{{Opposite}}{{Adjacent}}$
$ \Rightarrow \tan \theta = \dfrac{r}{h}$ ------($5$)
Since the equations ($4$) and ($5$) are identical they are equated to get:
$\dfrac{{m{v^2}}}{{mgr}} = \dfrac{r}{h}$
The common term,$m$, is not cancelled yet because our aim is to find out an equation for the centripetal force of the bob and hence we manipulate it to get the value of centripetal force. Hence the equation becomes:
$\dfrac{{m{v^2}}}{r} = \dfrac{{mgr}}{h}$
From equation ($1$)
$ \Rightarrow {F_c} = \dfrac{{mgr}}{h}$ ------($6$)

From the above diagram of the triangle ABC we can see that by applying Pythagoras theorem we get the value for $h$ in terms of the length of the string and the radius of the path. By considering triangle ABC we get:
By Pythagoras theorem:
${L^2} = {h^2} + {r^2}$
$ \Rightarrow {h^2} = {L^2} - {r^2}$
By taking square root on both sides we get:
$ \Rightarrow h = \sqrt {{L^2} - {r^2}} $ ------($7$)
By substituting equation ($7$) in ($6$) we get:
${F_c} = \dfrac{{mgr}}{{\sqrt {{L^2} - {r^2}} }}$
Hence the centripetal force acting on the bob of the conical pendulum is given by $\dfrac{{mgr}}{{\sqrt {{L^2} - {r^2}} }}$.

Therefore, the correct option is option A.

Note:The centripetal force is not a new force; it comes into play whenever a body exhibits circular motion. The horizontal and vertical components of force only come into picture when angle of inclination or an angle from the body in motion is created, for example a body sliding down an inclined plane will have these components. The force components will have to be considered only when there is a force (which in this case is the tension in the string) acting at an angle to the body.